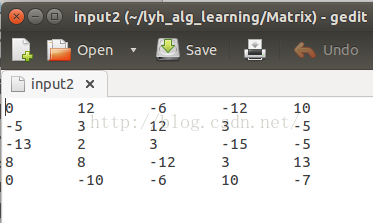
用它求逆後就變成這樣了：
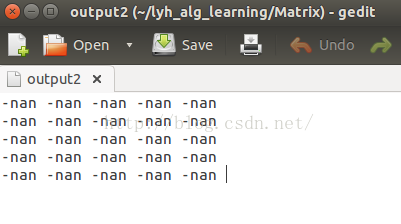可以看到我的求逆程序報錯了，顯示not a number，這是因為這個隨機生成的數組是不可逆的。因此我就想編寫一個能生成任意大小方陣的程序。
首先我們要生成一個任意大小的可逆方陣，再把它按照一定的格式寫入文件中。其實難點只有一個，就是如何構造可逆矩陣。我在網上找到了兩種解決辦法：
（1）生成隨機數矩陣後，再根據行列式值或者秩等條件判斷其是否可逆。
（2）先得到單位矩陣後在對其進行有限次的初等行變換。
運氣不好的話，第一種方式的開銷會很大，因此我們選擇第二種方式。但是，在第二種方式中也存在著如下問題：
（1）如何進行初等行變換才能使最後的結果正確
（2）如何使初等變換後的矩陣看起來更勻稱
下面我來解釋這兩點是啥意思。所謂正確就是在計算時沒有出現越界，溢出等情況，因為當矩陣中的數字比較大的時候，進行初等行變換的結果可能會使某些數字過大從而超過計算機能表示的精度導致溢出；所謂勻稱是指一個規模很大的矩陣中不會出現全是零或者某一大片扎堆是零另一部分非零。當然對於矩陣求逆來說，第一點是必須要滿足的，第二點我們暫且作為功能性需求。
好了，下面我來介紹一下我的思路。
當我們得到單位矩陣之後，就要考慮對其進行初等行變換了，無非就是交換兩行位置，將一行中所有的元素同乘以一個數，還有就是將一行中所有的元素同乘一個數後再加到另一行上，我的思路是，隨機的選取一個主行（行數當然要在0~n-1之間，n是方陣的行列數），然後進行隨機次數的行變換，但是行變換我僅采用“將一行中所有的元素乘以一個數之後再加到另一行上”這種方式，在每次初等行變換中執行乘法和加法之前要檢測結果是否會溢出。
int main(int argc, char* argv[])
{
int k = 0;
int n = 0;
int flag = 0;
int** array;
printf("Please input the line and row number of the matrix:\n");
scanf("%d",&n);
//Create matrix
printf("Start create a %d * %d matrix.\n",n,n);
array = (int**)malloc(sizeof(int*)*n);
for(k = 0; k < n; ++k)
{
array[k] = (int*)malloc(sizeof(int)*n);
}
printf("If you want get an identity matrix, please input 0, while if you want an invertible matrix, just input 1.\n");
scanf("%d",&flag);
if(flag == 0)
{
printf("Your input word is %d, so you want an identity matrix:\n",flag);
//get indentity matrix
getIdentityMatrix(n, array);
//put indentity matrix into file
putIdentityMatrixIntoFile(n, array);
//print identity matrix
printIdentityMatrix(n, array);
}
else if(flag == 1)
{
printf("Your input word is %d, so you want an invertible matrix:\n",flag);
//get indentity matrix
getIdentityMatrix(n, array);
//get invertible matrix
getInvertibleMatrix(n, array);
//put invertible matrix into file
putInvertibleMatrixIntoFile(n, array);
//print invertible matrix
printInvertibleMatrix(n, array);
}
else
{
printf("Error: You input a wrong number!\n");
return -1;
}
//free matrix
printf("Free matrix.\n");
freeMatrix(n, array);
return 1;
}
注：代碼中最後出現的freeMatrix函數是我專門為了釋放數組內存寫的，代碼如下：
void freeMatrix(int n, int** array)
{
int k = 0;
for(k = 0; k < n; ++k)
{
free(array[k]);
}
free(array);
}
void getIdentityMatrix(int n, int** array)
{
int r = 0;
int c = 0;
for(r = 0; r < n; ++r)
{
for(c = 0; c < n; ++c)
{
if(r == c)
array[r][c] = 1;
else
array[r][c] = 0;
}
}
}
mainRowNum = (int)(rand()%（n-1）);這句話是隨機的在矩陣0~n-1行中選擇一個主行作初等行變換，第一個循環是將主行中的元素進行一定的處理
array[mainRowNum][k])*((int)(rand()%5 - 10)後存入中介數組tempArray中（處理方式是我隨便寫的，也可以是別的運算方式）。 而這一句：
((UINT16_MAX - (array[mainRowNum][k])*((int)(rand()%5 - 10))) < 0) || ((UINT16_MAX*(-1)) - (array[mainRowNum][k])*((int)(rand()%5 - 10)) > tempArray[k])則是為了判斷采用上述處理方式對矩陣元素進行運算後，元素數值是否會溢出。（如果你想了解更多，請看這裡：點擊打開鏈接） 第二個循環的作用是遍歷矩陣中所有行，然後令處理過後主行和其他所有的行依次進行相加，這裡也進行了溢出判斷。 最後不要忘了釋放內存喲~
void getInvertibleMatrix(int n, int** array)
{
int i = 0;
int j = 0;
int k = 0;
int mainRowNum = 0;
int* tempArray = NULL;
srand((int)time(NULL));
int transformTime = (int)(rand()%1000);
printf("We will do %d times tansformation.\n",transformTime);
tempArray = (int*)malloc(sizeof(int)*n);
for(i = 0; i < transformTime; ++i)
{
mainRowNum = (int)(rand()%（n-1）);
for(k = 0; k < n; ++k)
if(((UINT16_MAX - (array[mainRowNum][k])*((int)(rand()%5 - 10))) < 0) || ((UINT16_MAX*(-1)) - (array[mainRowNum][k])*((int)(rand()%5 - 10)) > tempArray[k]))
tempArray[k] = (array[mainRowNum][k]);
else
tempArray[k] = (array[mainRowNum][k])*((int)(rand()%5 - 10));
for(j = 0; j < n; ++j)
if(mainRowNum != j)
for(k = 0; k < n; ++k)
{
if(((UINT16_MAX - array[j][k]) < tempArray[k]) || ((UINT16_MAX*(-1)) - array[j][k] > tempArray[k]))
array[j][k] = array[j][k]/4;
else
array[j][k] = array[j][k] + tempArray[k];
}
}
free(tempArray);
}
int putInvertibleMatrixIntoFile(int n, int** array)
{
FILE* fp = NULL;
int i = 0;
int j = 0;
if((fp = fopen("input","w"))==NULL)
{
printf("Error: writing file error!\n");
return -1;
}
for(i = 0; i < n; ++i)
{
for(j = 0; j < n; ++j)
{
if(j != (n-1))
fprintf(fp,"%d\t", array[i][j]);
else
fprintf(fp,"%d", array[i][j]);
}
fputs("\n",fp);
}
fclose(fp);
return 1;
}
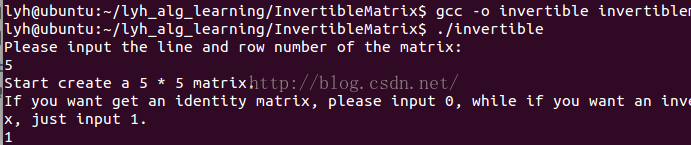
gcc -o invertible invertiblematrix.c我們以5*5的矩陣為例試一下
選擇1，讓其生成非單位矩陣的可逆矩陣
可以看出，做了780次行變換，只是矩陣有一列有很多0，看起來不太完美。
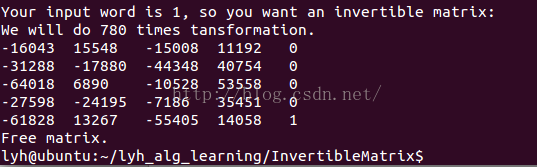用vim看一下我們得到的文件（名為input）：
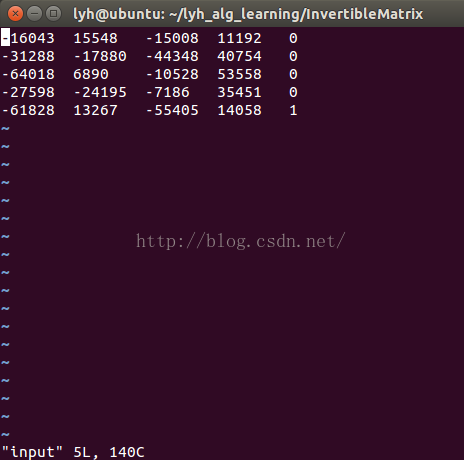初步成功~
