推薦文章:《淺析最大最小定理在信息學競賽中的應用》--周冬

講這部分之前,請先閱讀以上的文章(講得十分好%%%)(當然閱讀到27頁就好了)
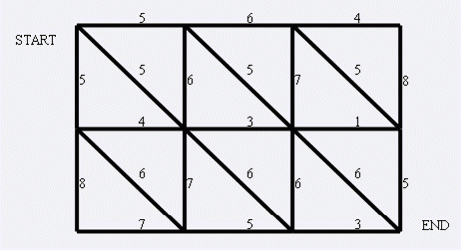
讀完後,我們發現這道題完全可以用其對偶圖來跑最短路。
原圖 對偶圖
面數 x 面數 y
點數 y 那麼其對偶圖中 點數 x
邊數 z 邊數 z
面數和點數正好相反。
將原圖的起點和終點連接起來,建立一個新的面(這是必須的)。
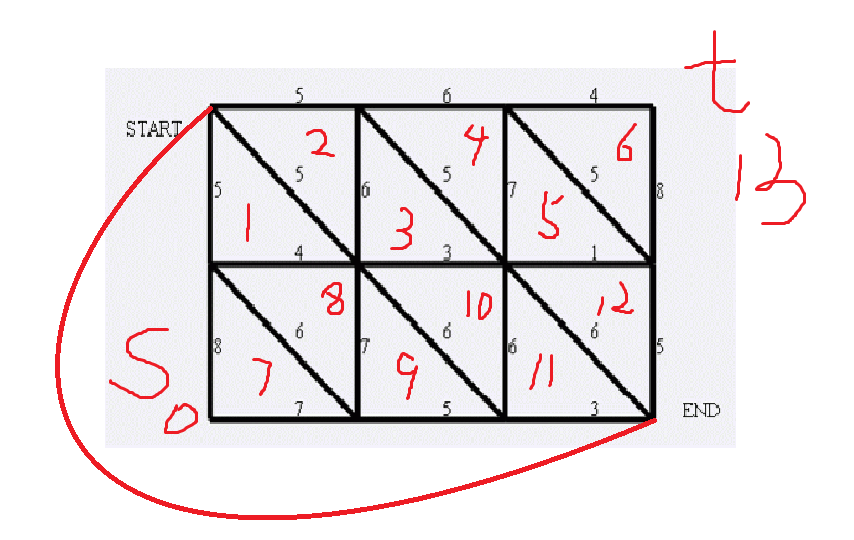
當然s點和t點之間是沒有邊的。
s和1,7,9,11之間有邊。
t和2,4,6,12之間有邊。
上面是我們建好的對偶圖,從左至右依次編號,關於對偶圖中面的編號,因為我們是按照橫邊,縱邊,斜邊的順序讀入的,所以我們一定要按照一定的方法對這些圖編號
我采用的是從左至右依次編號,因為我們可以很清楚當前邊連接的兩個點(原圖中的兩個面)所在的位置,因為這是平面圖,所以可以用歐拉公式來求出之前有多少點(
原圖中的面)。再加上這個點(原圖中的面(重要的事說三遍))在當前行中的位置就是它的編號。
只要原圖中的兩個面之間存在邊,那麼它的對偶圖中的兩個點就存在邊。
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int cnt, i, j, x, xx, xxx, h, t, s, hh[2010000], n, m, w;
bool dd[2010000];
int e, l[2010000], d[1010000], hhh, ww;
struct node
{
int v, next, z;
} b[6010000];
inline void add(int aa, int bb, int cc)//鄰接表,建雙向邊
{
b[++cnt].v = bb;
b[cnt].next = hh[aa];
b[cnt].z = cc;
hh[aa] = cnt;
b[++cnt].v = aa;
b[cnt].next = hh[bb];
b[cnt].z = cc;
hh[bb] = cnt;
}
void add1()
{
for(i = 1; i < m; ++i)
{
scanf("%d", &x);
add(i * 2, t, x);
}
for(i = 2; i < n; ++i)
{
for(j = 1; j < m; ++j)
{
scanf("%d", &x);
add((i - 1) * (m - 1) * 2 + j * 2, (i - 1) * (m - 1) * 2 + j * 2 - m * 2 + 1, x);//利用歐拉公式確定編號並建邊(下面的add函數也是如此)
}
}
for(j = 1; j < m; ++j)
{
scanf("%d", &x);
add(s, (n - 2) * 2 * (m - 1) + j * 2 - 1, x);
}
}
void add2()
{
for(i = 1; i < n; ++i)
{
scanf("%d", &x);
xx = (i - 1) * (m - 1) * 2 + 1;
add(s, xx, x);
for(j = 2; j < m; ++j)
{
scanf("%d", &x);
xx += 2;
add(xx - 1, xx, x);
}
scanf("%d", &x);
add(xx + 1, t, x);
}
}
inline void add3()
{
for(i = 1; i < n; ++i)
{
for(j = 1; j < m; ++j)
{
scanf("%d", &x);
add((i - 1) * (m - 1) * 2 + j * 2, (i - 1) * (m - 1) * 2 + j * 2 - 1, x);
}
}
}
//下面的spfa中一定要用循環隊列,省空間。不用的話空間開小(這很有可能畢竟1百萬個點)可能會被卡。
void spfa()
{
dd[s] = true;
h = 0;
w = 0;
memset(l,0x3f,sizeof(l));//將l數組賦成最大值
//hhh記錄的是我們用的是隊列中第幾個元素(實際上)
//ww記錄的是隊列中總共有幾個元素
l[s] = 0;
while(1)
{
if(hhh > ww)break;
h = hhh % 1000001;
w = ww % 1000001;
for(i = hh[s]; i; i = b[i].next)
{
e = b[i].v;
if(l[s] + b[i].z < l[e])
{
l[e] = l[s] + b[i].z;
if(!dd[e])w = ww % 1000000, d[++w] = e, ww++, dd[e] = true;
}
}
dd[s] = false;
h = hhh % 1000000;
s = d[++h];
hhh++;
}
}
int main()
{
scanf("%d %d", &n, &m);
if(n == m && n == 1)//特判
{
printf("0");
return 0;
}
s = 0;
t = 2 * (n - 1) * (m - 1) + 1;
add1();//讀入橫邊
add2();//讀入縱邊
add3();//讀入斜邊
spfa();//對其對偶圖求s————t的最短路
printf("%d", l[t]);
return 0;
}