整數拆分問題_C++，整數拆分_c

整數拆分問題_C++，整數拆分_c

一、問題背景

　  整數拆分，指把一個整數分解成若干個整數的和

　　如 3=2+1=1+1+1  共2種拆分

　　我們認為2+1與1+2為同一種拆分

二、定義

　　在整數n的拆分中，最大的拆分數為m，我們記它的方案數為 f(n,m)

　　即 n=x₁+x₂+······+x_k-1+x_k ，任意 x≤m

　　在此我們采用遞歸遞推法

三、遞推關系

　　1、n=1或m=1時

　　　　   拆分方案僅為 n=1 或 n=1+1+1+······

　　　　　f(n,m)=1

　　2、n=m時

　　　　　S₁選取m時，f(n,m)=1，即n=m

　　　　　S₂不選取m時，f(n,m)=f(n,m-1)=f(n,n-1)，此時討論最大拆分數為m-1時的情況

　　　　　可歸納 f(n,m)=f(n,n-1)+1

　　3、n<m時

　　　　　因為不能選取m，所以可將m看作n，進行n=m時的方案，f(n,m)=f(n,n)

　　4、n>m時

　　　　　S₁選取m時，f(n,m)=f(n-m,m)，被拆分數因選取了m則變為n-m，且n-m中可能還能選取最大為m的數

　　　　　S₂不選取m時，f(n,m)=f(n,m-1)，此時討論最大拆分數為m-1時的情況

　　　　　可歸納 f(n,m)=f(n,m-1)+f(n-m,m)

總遞推式為

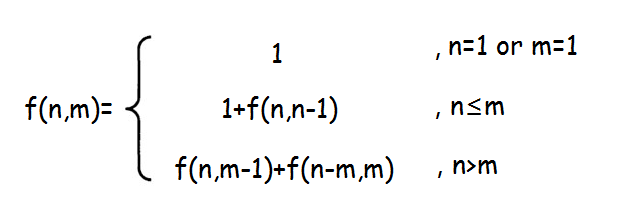
代碼如下

 1 #include <algorithm>
 2 #include <iostream>
 3 #include <cstdlib>
 4 #include <cstring>
 5 #include <cstdio>
 6 #include <cmath>
 7 using namespace std;
 8 
 9 int f(int n,int m)
10 {
11     if ((n!=1)&&(m!=1))
12         {
13             if (n>m) return f(n-m,m)+f(n,m-1);
14             else return 1+f(n,n-1);
15         }
16     else return 1;
17 }
18 void work()
19 {
20     int n,m;
21     cin>>n>>m;
22     cout<<f(n,m);
23 }
24 int main()
25 {
26     freopen("cut.in","r",stdin);
27     freopen("cut.out","w",stdout);
28     work();
29     return 0;
30 }

 此外還有母函數法，具體參考

http://blog.chinaunix.net/uid-26548237-id-3503956.html

版權所有，轉載請聯系作者，違者必究

QQ：740929894