今天集中把幾種排序的方法列一下，當然最出名的希爾，快排，歸並和其優化當然也是滿載
說到希爾排序的話，不得不先提到的就是插入排序了，希爾排序就是對直接插入排序的一種優化，下面就是直接插入排序的思想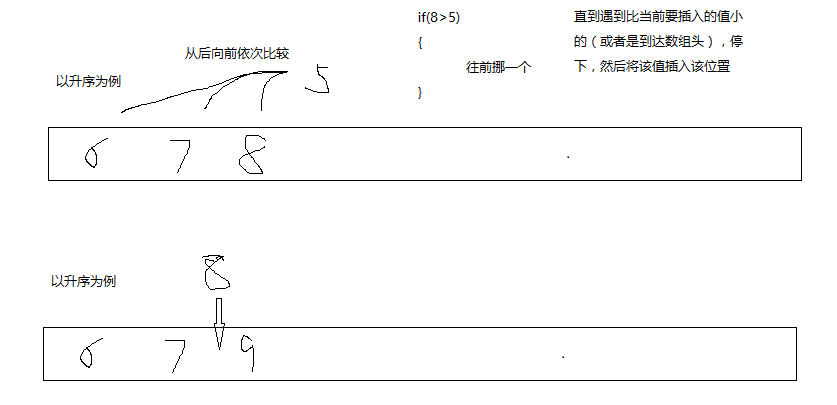
1 void InsertSort(int *a, size_t size)
2 {
3 assert(a);
4 for (int i = 1; i < size; ++i)
5 {
6 int index = i;
7 int tmp = a[index];
8 int end = index - 1;
9 while (end >= 0 && a[end]>tmp)
10 {
11 a[end + 1] = a[end];
12 end--;
13 }
14 a[end + 1] = tmp;
15 }
16 }
這就是直接插入排序的代碼，思想很簡單，代碼也很簡單
為什麼希爾排序比直接插入排序更加優化呢？當需要排序的數組過長的時候，有可能出現，插入數據的時候需要把數據插入到數組頭的位置，那麼數組中需要移動的數據就太多了，效率很低，但是當數組趨於有序的時候，直接插入排序的效率是很高的，所以希爾排序可以理解為直接插入排序的預排序，讓數組更趨於有序，希爾排序的最後一趟排序就是直接插入排序
將一個數組進行分組（就是隔幾個元素分為一組）如下圖
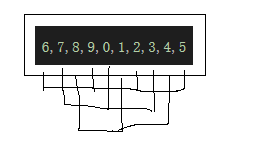圖中選擇每隔兩個元素分為一組，隔幾個元素（設為gap）一組是有講究的，會影響到排序的效率的，一會就推薦一種算法
分組之後，對每一組都進行插入排序，執行完一次所有的分組的插入排序之後算作完成一趟排序，然後減少gap的值，直到最後一次gap的值會變為1，成為直接插入排序
下面是代碼
1 void ShellSort(int *a,size_t size)
2 {
3 assert(a);
4 int gap = size;
5 while (gap > 1)
6 {
7 gap = gap / 3 + 1;
8 for (int i = gap; i < size; ++i)
9 {
10 int index = i;
11 int tmp = a[index];
12 int end = index - gap;
13 while (end >= 0 && a[end]>a[index])
14 {
15 a[end + gap] = a[end];
16 end -= gap;
17 }
18 a[end + gap] = tmp;
19 }
20 }
21 }
每次對gap的值進行gap=gap/3+1，為啥？因為比較優，具體應該就是數學問題了，我就不太清楚了。。。。
接下來是選擇排序，選擇選擇，就是每一次選出最大（小）值，然後交換到最高（低）的位置，優化！一次不僅可以選出最小的值，還可以選出最大的，同時選出，同時交換，可以提高效率
1 void SelectSort(int *a,size_t size )
2 {
3 assert(a);
4 int min;
5 int max;
6 for (int i = 0; i< size; i++)
7 {
8 min = i;
9 max = size - 1 - i;
10 for (int j = i + 1; j< size - i; j++)
11 {
12 if ( a[min]> a[j])
13 {
14 min = j;
15 }
16 if ( a[max]< a[j])
17 {
18 max = j;
19 }
20 }
21 swap(a[i], a[min]);
22 swap(a[size - 1 - i], a[max]);
23 }
24 }
思想啥的就不貼了，畢竟是比較簡單和基礎的排序了
接下來就是堆排序了！什麼是堆，這裡我就進行簡單的介紹了，堆的本質是一個數組，將這個數組看成一個二叉樹，很抽象，來個圖
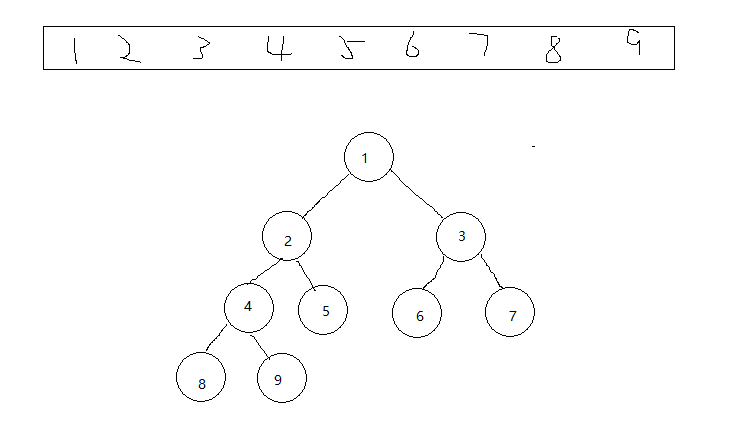
順序把數組弄成二叉樹，大堆（每個父親節點都比孩子節點的值要大），小堆（每個父親節點都比孩子節點的值要小，上圖就是一個小堆），所謂的堆排序就是把待排序的數組先建堆
每一次交換之後將調整的范圍縮小一個，這樣就能保證，每次交換到最後的數都是大數，並到了自己應該到的位置上去，建堆的過程用到向下調整，，每一次交換之後也要向下調整，堆是一種數據結構，這裡就不詳解了，之後會整理出堆來，這裡介紹堆排序的思想和代碼
1 void AdjustDown(int *a, size_t size, int root)
2 {
3 assert(a);
4 int child = root * 2 + 1;
5 while (child < size)
6 {
7 if (child + 1 < size && a[child + 1] > a[child])
8 {
9 child++;
10 }
11 if (a[child]>a[root])
12 {
13 swap(a[child], a[root]);
14 root = child;
15 child = root * 2 + 1;
16 }
17 else
18 {
19 break;
20 }
21 }
22 }
23
24
25 void HeapSort(int *a, size_t size)
26 {
27 assert(a);
28 for (int i = (size - 2) / 2; i >= 0; --i)
29 {
30 AdjustDown(a, size, i);
31 }
32 for (int i = size - 1; i >= 0; --i)
33 {
34 swap(a[0], a[i]);
35 AdjustDown(a, i, 0);
36 }
37 }
接下來就是快排了！！這個被譽為十大算法的家伙！！
快排的思想是拆分遞歸，直到遞歸到最深層（就一個元素）
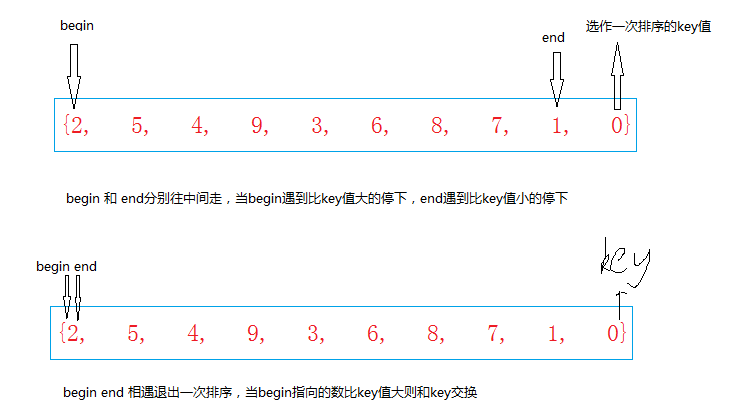
1 int PartionSort(int *a,int left,int right)
2 {
3 int MidIndex = GetMidIndex(a, left, right);
4 swap(a[MidIndex], a[right]);
5 int key = a[right];
6 int begin = left;
7 int end = right - 1;
8 while (begin < end)
9 {
10 while (begin < end && a[begin] <= key)
11 {
12 ++begin;
13 }
14 while (begin < end && a[end] >= key)
15 {
16 --end;
17 }
18 if (begin < end)
19 {
20 swap(a[begin], a[end]);//begin<end，比key值小的和比key值大的交換
21 }
22 }
23 if (a[begin] > key)
24 {
25 swap(a[begin], a[right]);
26 return begin;
27 }
28 return right;
29 }
30
31 void QuickSort(int *a,int left,int right)
32 {
33 assert(a);
34 if (right - left < 1)
35 {
36 return;
37 }
38 int boundary = PartionSort(a,left,right);
39 QuickSort(a, left, boundary-1);
40 QuickSort(a, boundary + 1, right);
41
42 }
但是不夠優化，當每次取的key值恰好比較接近最大值或者最小值的時候，分界遞歸的時候就會出現分布不均勻，導致效率低下，當劃分成兩邊相等的時候自然比較好，所以加上這個部分會比較好
1 int GetMidIndex(int *a, int left, int right)
2 {
3 assert(a);
4 int mid = left + (right - left) / 2;
5 if (a[left] < a[right])
6 {
7 if (a[mid] < a[left])
8 {
9 return left;
10 }
11 else if (a[mid] < a[right])
12 {
13 return mid;
14 }
15 else
16 return right;
17 }
18 else
19 {
20 if (a[mid] < a[right])
21 {
22 return right;
23 }
24 else if (a[mid] < a[left])
25 {
26 return mid;
27 }
28 else
29 return left;
30 }
31 }
三數取中法，代碼已經更新過了，所以上邊的快排已經是用三數取中優化過的
當快排遞歸到比較深層的時候，被分成小部分的區間內已經趨於有序了，那麼采用直接插入排序就可以有效的提高效率！！具體做法就是在QuickSort中的if部分修改，改掉遞歸結束條件，然後加上直接插入排序的代碼就好了
這個不能算是優化，思想有些不同，這次是從同一邊走采用cur和prev兩個參數，外層的遞歸還是不變的，只是一次排序不同了
1 int PartionSort2(int *a,int left,int right)
2 {
3 int key = a[right];
4 int cur = left;
5 int prev = left - 1;
6 while (cur < right)
7 {
8 if (a[cur] < key && prev++ != cur)
9 {
10 swap(a[prev], a[cur]);
11 }
12 cur++;
13 }
14 swap(a[prev], a[cur]);
15 return prev;
16 }
最後key值還是會跑到大概中間的位置，和他自己應該在的地方比較接近
最後一個排序就是歸並排序啦！
歸並排序一上來就將數組分割成兩部分，然後不停的分割，直到一個元素不能再分位置，然後開始合並相鄰的兩個元素，合並之後當然是有序的，有序之後就可以回到上一層，然後不斷的進行合並，最後整個數組都有序啦，也就是說要想合並，兩個部分都必須是有序的才行。
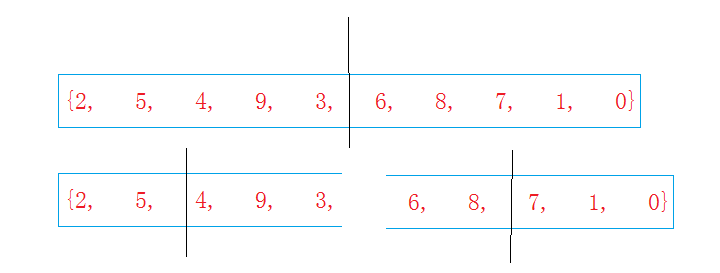
就是類似這樣的
思想還是不太難理解的
實現這樣的思想需要開辟輔助空間，因為當兩部分有序的數組合並之後還要是有序的才行，需要一個同等大小的數組暫存一下數據
1 void MergeSelection(int *a, int *tmp, int begin1, int end1, int begin2, int end2)
2 {
3 int index = begin1;
4 while (begin1 <= end1 && begin2 <= end2)
5 {
6 if (a[begin1] < a[begin2])
7 {
8 tmp[index++] = a[begin1++];
9 }
10 else
11 tmp[index++] = a[begin2++];
12 }
13 while (begin1 <= end1)
14 {
15 tmp[index++] = a[begin1++];
16 }
17 while (begin2 <= end2)
18 {
19 tmp[index++] = a[begin2++];
20 }
21 }
22
23
24 void MergeSort(int *a ,int *tmp,int left,int right)
25 {
26 int mid = left + (right - left) / 2;
27 if (left < right)
28 {
29
30 MergeSort(a, tmp, left, mid);
31 MergeSort(a, tmp, mid + 1, right);
32 MergeSelection(a, tmp, left, mid, mid + 1, right);
33
34 memcpy(a + left, tmp + left, sizeof(int)*(right - left + 1));
35 }
36 }
tmp是我在測試用例中就開辟好的，直接作為參數傳進去
