#01、引言，我們知道算式計算的問題是棧裡面一個非常經典的題目。但是用棧來實現是一個非常麻煩的過程，第一要解決算式判斷，是否為符合規則的算式，第二要由中最表達式轉化為後綴表達式。這兩個部分是棧實現計算算式表達式的比較復雜的地方。不僅如此，棧實現裡面的各種運算符的優先級，各種條件判斷，可以說是麻煩的要命。但是，實際上有一種數據結構比棧更適合解決這類問題。可以說是得天獨厚的優勢。對，就是二叉樹。例如一個表達式：1+2*3-4/5
我們構造這樣一個二叉樹
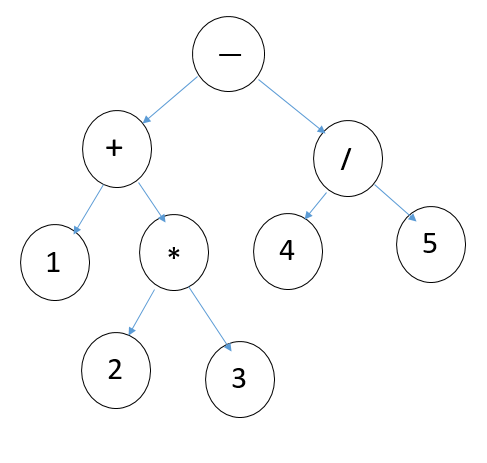當構造這樣一個二叉樹之後，解決表達式的值的方法，也就浮出水面了，把2和3相乘，存到*的節點中，然後再和1相加，存到+的節點中.....最後根節點-節點中存放的就是最後的計算結果。就是葉子節點執行其雙親節點的運算，結果存到雙親節點中。
#02、選二叉樹作為算法的存儲結構有什麼好處。
這主要有兩個方面的好處，這也是針對於棧算法的兩個麻煩的地方。
<1>//免除了算式表達式的檢查過程。為什麼能免除檢查，表達式的規范性呢？並不是不需要檢查，而是檢查的過程就包含在創建二叉樹的過程。認真分析這棵二叉樹，我們會發現，所有的葉子節點必須是操作數節點，而所有的非葉子節點必須是運算符節點，否則表達式的結構一點不正確，創建二叉樹的過程就可以對表達式經行檢查。表達式是否正確也只取決於兩個方面，第一、表達式的結構是否正確，比如不能出現2*+6這樣的表達式，第二、表達式的數據是否正確，例如不能出現1+2.2.3這樣的表達式，2.2.3不是一個符合規則的數據。而數據的檢查，也可以在給葉子節點賦值的時候檢查。所以避免的單獨經行表達式檢查的繁瑣。
<2>//不需要轉化為後綴表達式再經行表達式結果的計算，這也是得益於二叉樹這種結構的天然優勢，自我感覺就完全是為這種算法題設計的，天造地設嘛！
#03、算法實現
0x001、數據結構的定義：
1 #define Maxsize 100
2 //定義數據元素類型
3 typedef char elemtype;
4 //定義二叉樹數據變量
5 typedef union
6 {
7 char Operator;
8 double date;
9 }perdate;
10 //定義二叉樹鏈式存儲結構
11 typedef struct node
12 {
13 perdate DATE;//用union類型存運算符或操作數
14 struct node *lchild;
15 struct node *rchild;
16 }btnode;
1 struct op
2 {
3 char opration;
4 int index;//括號層數//當這個index被標記為-1時，就不會再次被查找到
5 int locate;//op的位置
6 };
用union定義一個perdate類型，用來分別記錄操作數和運算符。op是查找運算符時用，從後往前查找，括號級數最低的作為根節點來創建二叉樹。
0x002、實現的函數
//查找op，並填充Aop數組 int Sortop(char str[], op Aop[], int &index); //將字符串轉化為浮點數 double str_to_flaot(char strpoly[], int p,int q); //判斷數組是不是1.2類型，就是只有數據 bool isdate(char str[],int p,int q);//p,q指向str的開始和結尾處 //判斷str是否為運算符和括號 bool isoprater(char str[],int p,int q);//p,q指向str的開始和結尾處 //用算數表達式創建二叉樹 void Createbtnode(btnode *b, char *str, int p, int q,int tail);//p,q指向str的開始和結尾處；tail是Aop的尾指針 //計算二叉樹算式的結果 double Comp(btnode *b);
0x003、main函數，整個算法過程簡述
#include"標頭.h" int index = 0;//記錄最大的括號層數 struct op Aop[Maxsize];
1 int main()
2 {
3 btnode * b;
4 b = new btnode;
5 char str[Maxsize];
6 cout << "算式計算器[張安源]" << endl;
7 while(true)
8 {
9 cout << "[Type \"exit\" to exit]" << endl << "請輸入你要求的表達式：" << endl;
10 cin.getline(str, Maxsize);
11 if (strcmp("exit", str) == 0) break;//如果輸入的是exit則退出
12 else
13 {
14 int tail = Sortop(str, Aop, index);//整理得到Aop的結構數組
15 Createbtnode(b, str, 0, strlen(str) - 1, tail);
16 double result = Comp(b);
17 cout << result << endl;
18 }
19 }
20 }
一直循環，讓用戶輸入一個表達式，當輸入為exit時，退出循環。Sortop函數將表達式的操作符的括號層數和其在表達式的位置經行記錄到Aop數組裡面，返回值是最大的括號層數。然後由Createbtnode函數創建一個二叉樹b。comp求出二叉樹表達式的結構，然後輸出結果。大致的過程是這樣，但是裡面卻還包含了一些實現的細節，具體代碼是怎麼實現的就不啰嗦了，看代碼比講解跟方便。
0x004、整個project。
<1>Header.h
1 #pragma once
2 #include<iostream>
3 using namespace std;
4 #define Maxsize 100
5 //定義數據元素類型
6 //*********int check = 0;//作為判斷表達式是否正確的標記
7 typedef char elemtype;
8 //定義二叉樹數據變量
9 typedef union
10 {
11 char Operator;
12 double date;
13 }perdate;
14 //定義二叉樹鏈式存儲結構
15 typedef struct node
16 {
17 perdate DATE;//用union類型存運算符或操作數
18 struct node *lchild;
19 struct node *rchild;
20 }btnode;
21 //定義查找運算符的結構數組
22 struct op
23 {
24 char opration;
25 int index;//括號層數//當這個index被標記為-1時，就不會再次被查找到
26 int locate;//op的位置
27 };
28 extern int index;
29 extern struct op Aop[Maxsize];
30 //******************************************************
31 //查找op，並填充Aop數組
32 int Sortop(char str[], op Aop[], int &index);
33 //將字符串轉化為浮點數
34 double str_to_flaot(char strpoly[], int p,int q);
35 //判斷數組是不是1.2類型，就是只有數據
36 bool isdate(char str[],int p,int q);//p,q指向str的開始和結尾處
37 //判斷str是否為運算符和括號
38 bool isoprater(char str[],int p,int q);//p,q指向str的開始和結尾處
39 //用算數表達式創建二叉樹
40 void Createbtnode(btnode *b, char *str, int p, int q,int tail);//p,q指向str的開始和結尾處；tail是Aop的尾指針
41 //計算二叉樹算式的結果
42 double Comp(btnode *b);
<2>op.cpp
1 #include"標頭.h"
2 //查找op，並填充Aop數組
3 int Sortop(char str[], op Aop[], int &index)
4 {
5 int j = 0;//記錄Aop的top
6 int i;
7 int ind = 0;//記錄括號層數
8 for (i = 0; str[i] != '\0'; i++)
9 {
10 if (str[i] == '(')
11 ind++;
12 else if (str[i] == ')')
13 ind--;
14 else if (str[i] == '+' || str[i] == '-' || str[i] == '*'||str[i]=='/' || str[i] == '^')
15 {
16 Aop[j].opration = str[i];
17 Aop[j].index = ind;
18 Aop[j].locate = i;
19 j++;
20 }
21 index = (index > ind) ? index : ind;
22 }
23 return j;
24 }
25 //將字符串轉化為浮點數
26 double str_to_flaot(char strpoly[], int p,int q)
27 {
28 if (strpoly[p] == '(')
29 p++;
30 if (strpoly[q] == ')')
31 q--;
32 //判斷小數點前有幾位數字
33 int index = 0;
34 int temp = p;//保存原來的p值
35 double n = 0;//最後的浮點數
36 for (;( p <= q)&&(strpoly[p]!='.'); p++) index++;
37 p = temp;
38 for (; p<=q; p++)
39 {
40 if (strpoly[p] == '.') continue;
41 index--;
42 n = n + ((double)(strpoly[p] - '0'))*(pow(10, index));
43
44 }
45 return n;
46 }
47 //判斷數組是不是1.2類型，就是只有數據//忽略括號
48 bool isdate(char str[],int p,int q)
49 {
50 int i;
51 int index = 0;
52 for (i = p; i<=q; i++)
53 {
54 if (str[i] == '.')
55 index++;
56 if (str[i] == '+' || str[i] == '-' || str[i] == '*' ||str[i]=='/' || str[i] == '^')
57 return false;
58 }
59 if (index== 0 || index == 1)
60 {
61 return true;
62 }
63 else
64 abort();
65 }
66 //判斷str是否為運算符和括號
67 bool isoprater(char str[],int p,int q)
68 {
69 if ((p==q)&&(str[p] == '(' || str[p] == ')' || str[p] == '*'||str[p]=='/' || str[p] == '^' || str[p] == '+' || str[p] == '-'))
70 return true;
71 else
72 return false;
73 }
74 //用算數表達式創建二叉樹
75 void Createbtnode(btnode *b, char *str, int p, int q,int tail) //由str串創建二叉鏈
76 { //p,q分別標志Aop的首尾
77 int i = 0;
78 int j = 0;//
79 int find=0;
80 if (isdate(str,p,q))//str為1.3類型
81 {
82 //創建頭節點，並將數據位置為str_to_double
83 b->DATE.date = str_to_flaot(str,p,q);
84 b->lchild = NULL;
85 b->rchild = NULL;
86 }
87 else if (isoprater(str,p,q))//str為+、—、^、（、）、*
88 {
89 abort();
90 b->DATE.Operator = str[i];
91 b->lchild = NULL;
92 b->rchild = NULL;
93 }
94 ///***************************************************************
95 else
96 for (int temp = 0; temp <= index; temp++)
97 {
98 for (j = tail; j >=0; j--)//從後往前找，才符合運算的法則，前面先算後面後算
99 {
100 if (Aop[j].index == temp && ((Aop[j].opration == '+')||(Aop[j].opration == '-')) && Aop[j].locate >= p&&Aop[j].locate <= q)
101 {
102 find++;
103 Aop[j].index = -1;//標志這個已經被找過了
104 btnode *lt, *rt;
105 lt = new btnode;
106 rt = new btnode;
107 b->lchild = lt;
108 b->rchild = rt;
109 b->DATE.Operator = Aop[j].opration;
110 Createbtnode(b->lchild, str, p, Aop[j].locate - 1,tail);
111 Createbtnode(b->rchild, str, Aop[j].locate+1, q,tail);
112 }
113 }
114 if(find==0)
115 for (j = tail; j >=0; j--)
116 {
117 if (Aop[j].index == temp && ((Aop[j].opration == '*')||(Aop[j].opration=='/')) && Aop[j].locate >= p&&Aop[j].locate <= q)
118 {
119 find++;
120 Aop[j].index = -1;//標志這個已經被找過了
121 btnode *lt, *rt;
122 lt = new btnode;
123 rt = new btnode;
124 b->lchild = lt;
125 b->rchild = rt;
126 b->DATE.Operator = Aop[j].opration;
127 Createbtnode(b->lchild, str, p, Aop[j].locate - 1,tail);
128 Createbtnode(b->rchild, str, Aop[j].locate+1, q,tail);
129 }
130 }
131 if(find==0)
132 for (j = tail; j >=0; j--)
133 {
134 if (Aop[j].index == temp && (Aop[j].opration == '^') && Aop[j].locate >= p&&Aop[j].locate <= q)
135 {
136 Aop[j].index = -1;//標志這個已經被找過了
137 btnode *lt, *rt;
138 lt = new btnode;
139 rt = new btnode;
140 b->lchild = lt;
141 b->rchild = rt;
142 b->DATE.Operator = Aop[j].opration;
143 Createbtnode(b->lchild, str, p, Aop[j].locate - 1,tail);
144 Createbtnode(b->rchild, str, Aop[j].locate+1, q,tail);
145 }
146 }
147 }
148 }
149 //計算二叉樹算式的結果
150 double Comp(btnode *b)
151 {
152 double v1, v2;
153 if (b == NULL) return 0;
154 if (b->lchild == NULL && b->rchild == NULL)
155 return b->DATE.date; //葉子節點直接返回節點值
156 v1 = Comp(b->lchild);
157 v2 = Comp(b->rchild);
158 switch (b->DATE.Operator)
159 {
160 case '+':
161 return v1 + v2;
162 case '-':
163 return v1 - v2;
164 case '*':
165 return v1*v2;
166 case '/':
167 if (v2 != 0)
168 return v1 / v2;
169 else
170 abort();
171 case '^':
172 return (pow(v1, v2));
173 default:
174 abort();
175 }
176 }
<3>main.cpp
1 #include"標頭.h"
2 int index = 0;//記錄最大的括號層數
3 struct op Aop[Maxsize];
4 int main()
5 {
6 btnode * b;
7 b = new btnode;
8 char str[Maxsize];
9 cout << "算式計算器[張安源]" << endl;
10 while(true)
11 {
12 cout << "[Type \"exit\" to exit]" << endl << "請輸入你要求的表達式：" << endl;
13 cin.getline(str, Maxsize);
14 if (strcmp("exit", str) == 0) break;//如果輸入的是exit則退出
15 else
16 {
17 int tail = Sortop(str, Aop, index);//整理得到Aop的結構數組
18 Createbtnode(b, str, 0, strlen(str) - 1, tail);
19 double result = Comp(b);
20 cout << result << endl;
21 }
22 }
23 }
#04算法測試
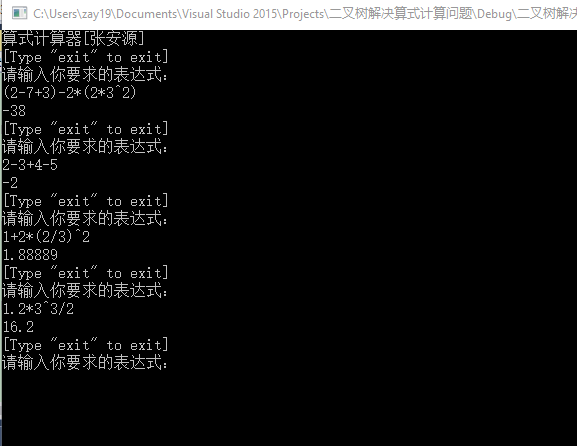
當輸入的表達式符合規則時，返回表達式的值。
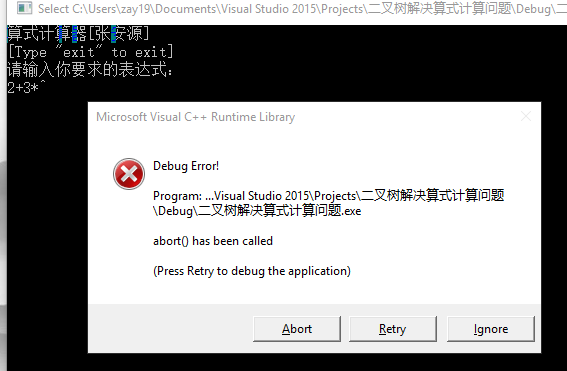
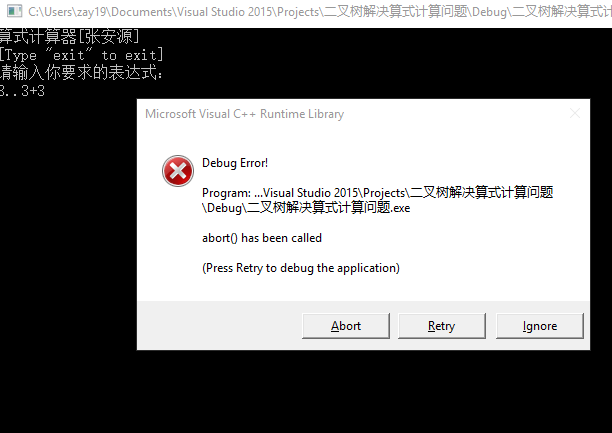
當輸入的表達式不符合規則時，則調用abort函數。
#05、總結
好的數據結構能事半功倍，要培養善於發現的思維，當有某個思路然後去實現它，另外要積累經驗。好好理解數據結構！
