聲明 :
僅一張圖片轉載於http://www.cnblogs.com/shuaiwhu/archive/2012/04/22/2464583.html,自己畫太麻煩了。。。那個博客的講解也很好,只是他用了指針的方式來定義線段樹,而我用了結構體,並且他講了線段樹的更高級的操作,若對線段樹的初級操作不理解,請繼續閱讀
線段樹作為一種十分常用的數據結構,在NOIP、NOI中廣泛的出現,所以在這裡對線段樹進行簡單的講解。
線段樹支持對一個數列的求和、單點修改、求最值(最大、最小)、區間修改(需要lazy標記,暫不講解)。這幾種操作,時間復雜度是(logn)級別的,是一種十分優秀的數據結構。因此其獲得了廣泛的應用。
定義:顧名思義,它是一種樹形結構,但每段不是平常所學的一個點一個點的樹,而是一條一條的線段,每條線段包含著一些值,其中最主要的是起始和結束點記作 l,r 即左端點和右端點。
那麼該如何劃分線段樹呢?我們采用二分的思想,即每次將一段取半,再進行接下來的操作,這樣綜合了操作的方便程度和時間復雜度。因為線段樹通過二分得來,所以線段樹是一顆二叉樹。這也方便了對兒子查找。下面是線段樹的圖,有利於理解:
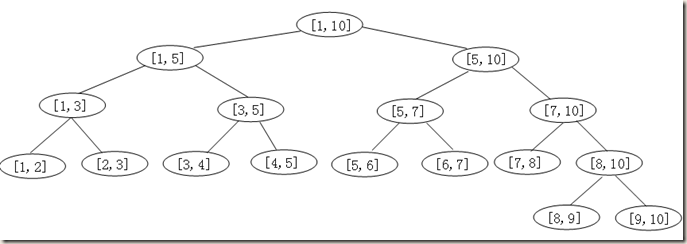
建樹:僅僅知道模型還是不夠的,建樹的過程是線段樹的關鍵(build(1,1,n))從一號開始,左端是1,右端是n
位運算 i<<1 等效於 i/2 (i<<1)|1 等效於 i/2+1 加速。。。
inline void update(int i)更新i節點維護的值(求和,最大……)
{
node[i].sum=node[i<<1].sum+node[(i<<1)|1].sum;
node[i].maxx=max(node[i<<1].maxx,node[(i<<1)|1].maxx);
}
inline void build(int i,int l,int r)//inline 還是加速
{
node[i].l=l;node[i].r=r;//左右端點為當前遞歸到的 l 和 r
if(l==r){//若l==r 則當前的樹節點是真正意義上的點
node[i].maxx=a[l];//最大值就是本身的值
node[i].sum=a[l];//區間的和就是本身的值
return;
}
int mid=(l+r)/2;//因為是二叉樹所以以中點為分割點
build(i<<1,l,mid);//根據二叉樹的知識,左兒子是i/2右兒子是i/2+1
build((i<<1)|1,mid+1,r);
update(i);
}
數列求和:這是線段樹的一個典型算法,其他的很多應用都是從中轉化的。
為了求和我們定義一個函數sum(int i,int l,int r) i 是開始的樹節點,我們默認為1。l 是區間的開始點,它的標號是在數列中的標號,r 是結束點其余同 l。帖下代碼:
inline int sum(int i,int l,int r)//inline 又是加速
{
if(node[i].l==l&&node[i].r==r)
return node[i].sum;//若樹節點的左右區間與查找區間相同,返回其維護的sum
int mid=(node[i].l+node[i].r)/2;//確定該樹節點的中點以確定繼續查找左兒子還是右兒子
if(r<=mid) return sum(i<<1,l,r);//若查找區間最右端小於中點,則該區間完全包含於左兒子中
else if(l>mid) return sum((i<<1)|1,l,r);//最左端大於中點,查找右兒子
else return sum(i<<1,l,mid)+sum((i<<1)|1,mid+1,r)
//若跨越中點,查找左兒子 l 到 mid ,和右兒子的 mid+1 到 r 並返回值
}
區間求最值和區間求和大致相同,自己看一下
inline int Max(int i,int l,int r)
{
if(node[i].l==l&&node[i].r==r)
return node[i].maxx;
int mid=(node[i].l+node[i].r)/2;
if(r<=mid) return Max(i<<1,l,r);
else if(l>mid) return Max((i<<1)|1,l,r);
else return max(Max(i<<1,l,mid),Max((i<<1)|1,mid+1,r));
}
單點更新:和區間不同,但基本思想還是一樣的。
inline void add(int i,int k,int v)//當前計算到的點為i,把數列中的第k個元素加v
{
if(node[i].l==k&&node[i].r==k){//因為更改的單點,所以左右端點均和k相等
node[i].sum+=v;
node[i].maxx+=v;
return;
}
int mid=(node[i].l+node[i].r)/2;
if(k<=mid) add(i<<1,k,v);//若k小於mid則k在樹節點i的左子樹中
else add((i<<1)|1,k,v);//反之
update(i);//更新
}
最後貼下全部的代碼基本可以做模板了。。
#include<iostream>
#include<cstdio>
using namespace std;
struct tree{
int l,r,sum,maxx;
};
tree node[100];
int n,m,a[100];
inline void update(int i)
{
node[i].sum=node[i<<1].sum+node[(i<<1)|1].sum;
node[i].maxx=max(node[i<<1].maxx,node[(i<<1)|1].maxx);
}
inline void build(int i,int l,int r)
{
node[i].l=l;node[i].r=r;
if(l==r){
node[i].maxx=a[l];
node[i].sum=a[l];
return;
}
int mid=(l+r)/2;
build(i<<1,l,mid);
build((i<<1)|1,mid+1,r);
update(i);
}
inline void add(int i,int k,int v)
{
if(node[i].l==k&&node[i].r==k){
node[i].sum+=v;
node[i].maxx+=v;
return;
}
int mid=(node[i].l+node[i].r)/2;
if(k<=mid) add(i<<1,k,v);
else add((i<<1)|1,k,v);
update(i);
}
inline int sum(int i,int l,int r)
{
if(node[i].l==l&&node[i].r==r)
return node[i].sum;
int mid=(node[i].l+node[i].r)/2;
if(r<=mid) return sum(i<<1,l,r);
else if(l>mid) return sum((i<<1)|1,l,r);
else return sum(i<<1,l,mid)+sum((i<<1)|1,mid+1,r);
}
inline int Max(int i,int l,int r)
{
if(node[i].l==l&&node[i].r==r)
return node[i].maxx;
int mid=(node[i].l+node[i].r)/2;
if(r<=mid) return Max(i<<1,l,r);
else if(l>mid) return Max((i<<1)|1,l,r);
else return max(Max(i<<1,l,mid),Max((i<<1)|1,mid+1,r));
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
build(1,1,n);
for(int i=1;i<=m;i++){
int c,a,b;
scanf("%d%d%d",&c,&a,&b);
if(c==1) printf("%d\n",sum(1,a,b));
else if(c==2) add(1,a,b);
else if(c==3) printf("%d\n",Max(1,a,b));
}
}