離散余弦變換(C++實現)

理論：

圖像處理中常用的正交變換除了傅裡葉變換外，還有其他一些有用的正交變換,其中離散余弦就是一種。離散余弦變換表示為DCT( Discrete Cosine Transformation)，常用於圖像處理和圖像識別等。

一維離散余弦變換

正變換

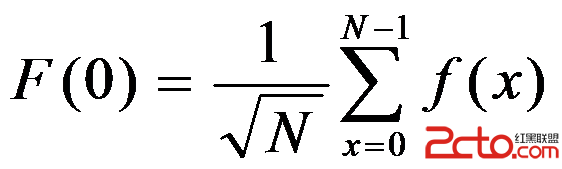(1)

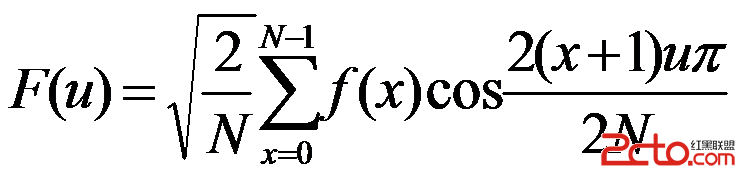(2)

式中F(u)是第u個余弦變換系數，u是廣義頻率變量,u=1,2,3......N-1; f(x)是時域N點序列, x=0,1,2......N-1

反變換

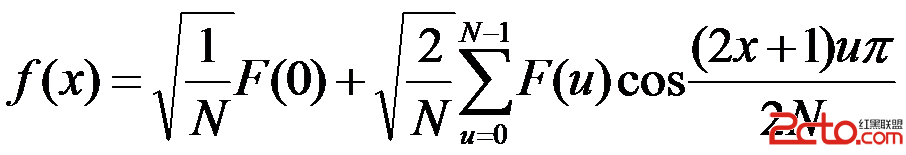（3）

顯然，式(1)式(2)和式(3)構成了一維離散余弦變換對。

二維離散余弦變換

正變換

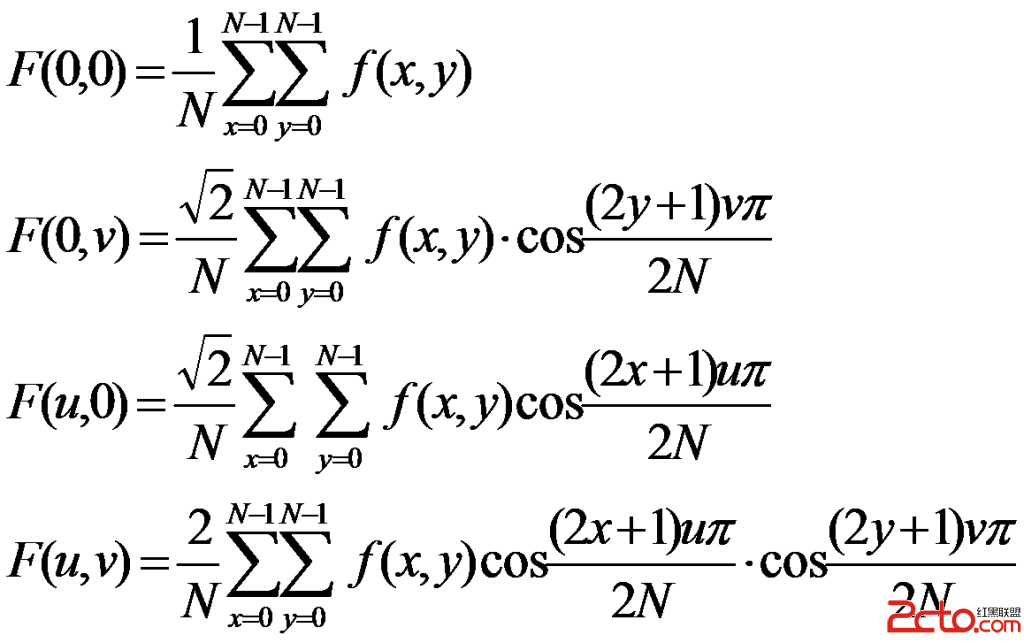（4）

式(4)是正變換公式。其中f(x,y)是空間域二維向量之元素， x,y=0,1,2,......N-1；F(u,v)是變換系數陣列之元素。式中表示的陣列為N×N

反變換

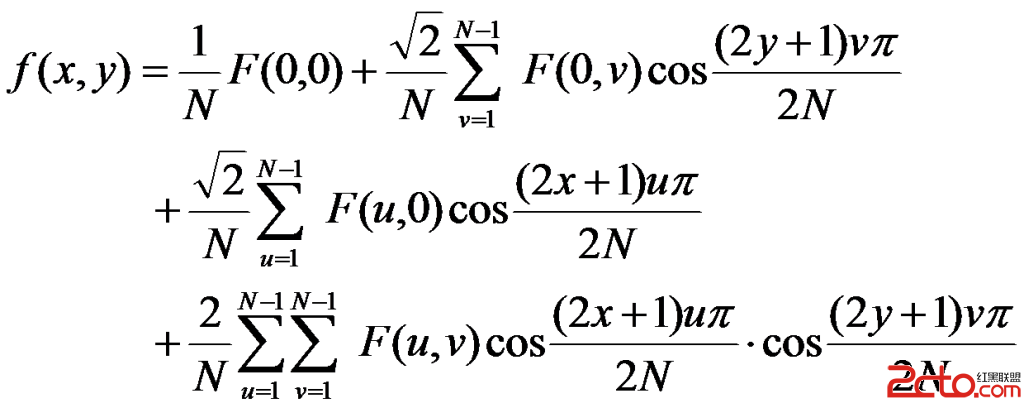（5）

式中的符號意義同正變換式一樣。式(4)和式(5)是離散余弦變換的解析式定義。

矩陣表示法

更為簡潔的定義方法是采用矩陣式定義。根據以上公式定義可知，離散余弦變換的系數矩陣可以寫成如下：

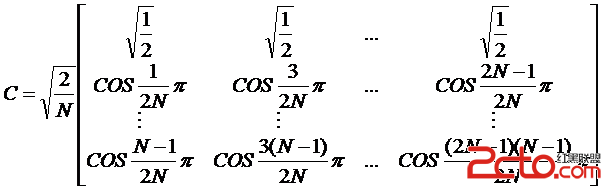
如果令N＝4，那麼由一維解析式定義可得如下展開式。

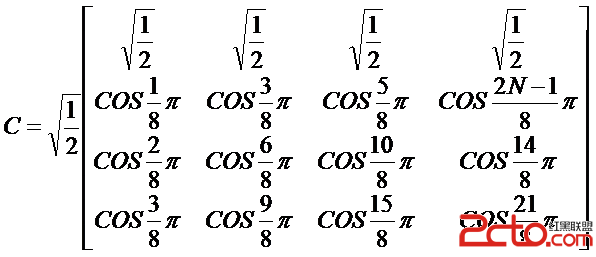
寫成矩陣式

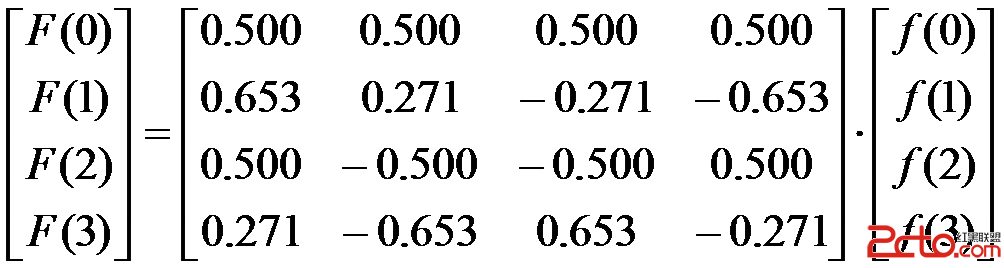
若定義F(u)為變換矩陣，A為變換系數矩陣，f(x)為時域數據矩陣，則一維離散余弦變換的矩陣定義式可寫成如下形式

[F(u)]=[A][f(x)] （6）

同理，可得到反變換展開式

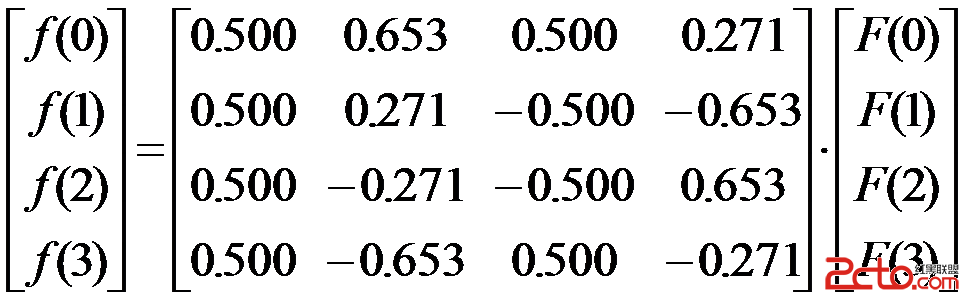
寫成矩陣式即

[f(x)]=[A]^T[F(u)] （7）

二維離散余弦變換也可以寫成矩陣式：

[F(u,v)]=[A][f(x,y)][A]^T （8）

[f(x,y)]=[A]^T[F(u,v)][A]

式中[f(x,y)]是空間數據陣列，A是變換系數陣列，[F(u,v)]是變換矩陣，[A]T是[A]的轉置。

對二維圖像進行離散余弦變換

由以上對二維離散余弦變換的定義及公式（7）可知，求二維圖像的離散余弦變換要進行以下步驟：

1.獲得圖像的二維數據矩陣f(x,y)；

2.求離散余弦變換的系數矩陣[A]；

3.求系數矩陣對應的轉置矩陣[A]T；

4.根據公式（7）[F(u,v)]=[A][f(x,y)][A]T 計算離散余弦變換；

C++代碼：

/*
	功能：獲取DCT系數
	n：矩陣大小
	quotient: 系數
	quotientT: 系數轉置
*/
void coefficient(const int &n, double **quotient, double **quotientT){
	double sqr = 1.0/sqrt(n+0.0);
	for(int i = 0; i < n; i++){
		quotient[0][i] = sqr;
		quotientT[i][0] =  sqr;
	}

	for(int i = 1; i < n; i++){
		for(int j = 0; j < n; j++){
			quotient[i][j] = sqrt(2.0/n)*cos(i*(j+0.5)*PI/n);  // 由公式得到
			quotientT[j][i] = quotient[i][j];
		}
	}

}
/*
	功能：兩矩陣相乘
	A和B：源輸入矩陣
	result：輸出矩陣
*/
void matrixMultiply(double **A, double **B, int n, double **result){  
	double t = 0;
	for(int i = 0; i < n; i++){
		for(int j = 0; j < n; j++){
			t = 0;
			for(int k = 0; k < n; k++)
				t += A[i][k]*B[k][j];   
			result[i][j] = t;
		}
	}
}

//  DCT變換
void DCT(Mat_ image, const int &n, double **iMatrix){
	for(int i = 0; i < n; i++){
		for(int j = 0; j < n; j++){
			iMatrix[i][j] = (double)image(i,j);
		}
	}

	// 為系數分配空間
	double **quotient = new double*[n];
	double **quotientT = new double*[n];
	double **tmp = new double*[n];
	for(int i = 0; i < n; i++){
		quotient[i] = new double[n];
		quotientT[i] = new double[n]; 
		tmp[i] = new double[n];
	}
	// 計算系數矩陣
	coefficient(n, quotient, quotientT);
	matrixMultiply(quotient, iMatrix, n, tmp);  // 由公式成績結果
	matrixMultiply(tmp, quotientT, n, iMatrix);

	for(int i = 0; i < n; i++){
		delete []tmp[i];
		delete []quotient[i];
		delete []quotientT[i];
	}
	delete []tmp;
	delete []quotient;
	delete []quotientT;
}