Stern-Brocot Tree
Time Limit: 3000/1000 MS (Java/Others) Memory Limit:
65535/32768 K (Java/Others)
Problem Description
vcr9wdBGoaM8YnI+CqGhoaHP1tTax+vE+rHgs8y8xsvjtdpu0NC1xMr9wdBGtcS49sr9oaM8YnI+CgoKIAo8YnI+CgpJbnB1dAoKoaGhocrkyOuw/LqstuDX6bLiytTTw8D9o6zDv9fpyuTI68r9vt3Kx9K7uPbV/dX7yv1uo6huPD0xMDAwMDAwo6mhowoKIAo8YnI+CgpPdXRwdXQKCqGhoaG21NPaw7/X6bXEsuLK1Mr9vt1uo6zH68rks/a12m7Q0LXEyv3B0Ea1xLj2yv2howoKIAo8YnI+CgpTYW1wbGUgSW5wdXQKCjxwcmUgY2xhc3M9"brush:java;">1
2
4
6
Sample Output
3
5
13
25
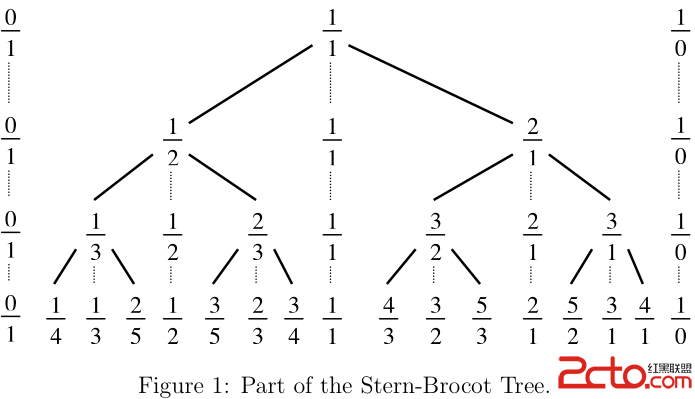
仔細看圖可以發現：對於每一行都可以看成是關於1/1對稱的兩部分，所以只需求出1/1左邊的個數就可求出這一行的個數。而左邊全部都是真分數，分母為x的真分數的個數就是x的歐拉函數值。n最大為1000000，所以可以遞推打表。
#include
const int N = 1000001;
int e[N];
__int64 a[N], res = 0;
void euler()
{
for(int i = 2; i < N; i++)
e[i] = 0;
e[1] = 1;
for(int i = 2; i < N; i++)
if(!e[i])
{
for(int j = i; j < N; j += i)
{
if(!e[j])
e[j] = j;
e[j] = e[j] / i * (i-1);
}
}
}
int main()
{
int i, n;
euler();
for(i = 1; i < N; i++)
{
res += e[i];
a[i] = res * 2 + 1;
}
while(~scanf("%d", &n))
printf("%I64d\n", a[n]);
return 0;
}
