在二維平面上的n個點中,如何快速的找出最近的一對點,就是最近點對問題。

初看這個題,可能感覺有點兒復雜。
方案一:蠻力法。數組中總共包含N個數,所以我們可以把平面內所有的點按X軸排序,然後依次算出後一個坐標與前面所有左邊的距離,然後用Min和position來記錄最近的距離和兩個坐標。該方案和在一維空間求兩個最近點的距離有點兒類似,其時間復雜度為:O(N*N).
方案二:在一維空間裡,我們知道如果數組有序,我們可以很快找出最近的兩個點。我們可以用O(N*logN)的時間復雜度來對數據進行排序[快,堆,歸]。排完序後只需要O(N)的時間復雜度就可以得到最小的差值。但是該方法不能用在二維,因為在二維空間中,X軸間距離最小的兩個點距離不一定是最短的,如下圖所示。
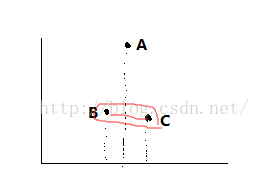
那還有什麼方法嗎?這裡我們采用了分治法。我們利用數組的中位數[中位數的求解細節可以參考這裡],將數組分成Left和Right兩個部分,要麼來自Right部分,要麼來自Left部分,或者來自Left和Right。這裡我們就可以將時間復雜度降低到O(N*logN)。
這裡主要復雜在合並的地方,其思想如下:
第一步:首先找出點集數據中的中位數median,按X坐標來劃分;用median對點集數據進行劃分,左邊的為data1,右邊的為data2;
第二步:對分成的兩部分分別求出data1和data2中的最近點對,記為:MinDis1和MinDis2;
第三步:求出data1和data2最近點對距離的較小值:MinDis = min{MinDis1,MinDis2};
第四步:找出data2中y值前6大的點[利用鴿巢原理,因為其距離不可能小於Min,而我們只考慮在Min*2*Min的方框內的數據],
對於data1中的點,與data2中的每一個點計算距離MinDisO, 如果MinDisO < MinDis,就改變MinDis的值,MinDis=MinDis0;說明在最小的距離一個來自左邊一個來自右邊,在合並的時候產生。
參考代碼如下:
#include <iostream>
#include <vector>
#include
#include <cmath>
using namespace std;
// 頂點信息
struct Point
{
double m_x, m_y;
Point():m_x(0.0),m_y(0.0) {}
Point(double x, double y):m_x(x),m_y(y){}
bool operator==(const Point& p) const
{return m_x==p.m_x && m_y==p.m_y;}
};
ostream& operator<<(ostream& os, const Point& p)
{
return os << "(" << p.m_x << "," << p.m_y << ")";
}
// 插入排序
template<class t,="" class="" pr="">
void insert_sort(vector<t> &vec, int l, int r, Pr pred)
{
int i, j;
for (i=l+1; i<=r; i++)
{
T tmp = vec[i];
for (j=i-1; j>=l && pred(tmp,vec[j]); j--)
vec[j+1]=vec[j];
vec[j+1] = tmp;
}
}
// 找到key所在的位置
template<class t="">
int get_position(vector<t> &vec, int l, int r, T key)
{
for (int i=l; i<=r; i++)
if (key == vec[i])
return i;
return -1;
}
// 按第一個元素對vec進行劃分
template<class t,="" class="" pr="">
int partition(vector<t> &vec, int l, int r, Pr pred)
{
int i, j;
for (i=l+1,j=l; i<=r; i++)
{
if (pred(vec[i],vec[l]))
{
++j;
swap(vec[i],vec[j]);
}
}
swap(vec[j],vec[l]);
return j;
}
// 順序統計得到第k個元素的值
template<class t,="" class="" pr="">
T select(vector<t> &vec, int l, int r, int k, Pr pred)
{
int n = r-l+1;
if (n==1)
{
if (k!=0)
printf("Out of Boundary!\n");
return vec[l];
}
// 找中位數的中位數作為分割點
int cnt = n/5;
int tcnt = (n+4)/5;
int rem = n%5;
vector<t> group(tcnt);
int i, j;
for (i=0,j=l; i<cnt; i++,j+="5)" {="" insert_sort(vec,="" j,="" j+4,="" pred);="" group[i]="vec[j+2];" }="" if="" (rem)="" j+rem-1,="" t="" key="select(group," 0,="" tcnt-1,="" (tcnt-1)="" 2,="" 找到分割點的位置="" int="" key_pos="get_position(vec," l,="" r,="" key);="" swap(vec[key_pos],="" vec[l]);="" 用分割點對數組進行劃分,小的在左邊,大的在右邊="" pos="partition(vec," x="pos" -="" l;="" (x="=" k)="" return="" key;="" else="" <="" select(vec,="" pos+1,="" k-x-1,="" pos-1,="" k,="" 計算點a和b的距離="" double="" dist(const="" point&="" a,="" const="" b)="" y="a.m_y-b.m_y;" sqrt(x*x+y*y);="" bool="" cmpx(const="" a.m_x="" b.m_x;="" cmpy(const="" a.m_y="" b.m_y;="" mindifferent(vector<point=""> p, int l, int r, vector<point> &result)
{
// 按中位數進行劃分後的子區域的元素個數都會減小到2或3,不會再到1
if ((r-l+1)==2)
{
result[0] = p[l];
result[1] = p[r];
if (cmpX(p[r],p[l])) swap(p[l], p[r]);
return dist(p[l], p[r]);
}
if ((r-l+1)==3)
{
insert_sort(p, l, r, cmpX);
double tmp1 = dist(p[l], p[l+1]);
double tmp2 = dist(p[l+1], p[l+2]);
double ret = min(tmp1, tmp2);
if (tmp1 == ret)
{
result[0] = p[l];
result[1] = p[l+1];
}
else
{
result[0] = p[l+1];
result[1] = p[l+2];
}
return ret;
}
// 大於3個點的情況
int mid = (r+l)>>1;
Point median = select(p, l, r, mid-l, cmpX);
vector<point> res1(2), res2(2);
double min_l = minDifferent(p, l, mid, res1);
double min_r = minDifferent(p, mid+1, r, res2);
double minum = min(min_l, min_r);
if (minum == min_l)
{
result[0] = res1[0];
result[1] = res1[1];
}
else
{
result[0] = res2[0];
result[1] = res2[1];
}
// 對[p[mid+1]-minum, p[mid]+minum]的帶狀區域按y排序
vector<point> yvec;
int i, j;
for (i=mid+1; i<=r; i++)
if (p[i].m_x - p[mid].m_x < minum)
yvec.push_back(Point(p[i]));
for (i=mid; i>=l; i--)
if (p[mid+1].m_x - p[i].m_x < minum)
yvec.push_back(Point(p[i]));
sort(yvec.begin(), yvec.end(), cmpY);
for (i=0; i<yvec.size(); i++)="" {="" 至多只有與其後最多7個點的距離會小於minum="" for="" (j="i+1;" j<yvec.size()="" &&="" yvec[j].m_y-yvec[i].m_y<minum="" j<="i+7;" j++)="" double="" delta="dist(yvec[i],yvec[j]);" if="" (delta="" <="" minum)="" minum="delta;" result[0]="yvec[i];" result[1]="yvec[j];" }="" return="" minum;="" int="" main()="" n,="" i,="" j,="" x,="" y;="" vector<point=""> result(2);
vector<point> input;
cout<<"please input the number of your data:"<<endl; cin="">> n;
cout<<"please input your data:"<<endl; for="" (i="0;" i<n;="" i++)="" {="" cin="">> x;
cin >> y;
input.push_back(Point(x,y));
}
double minum = minDifferent(input, 0, input.size()-1, result);
cout << "nearest point: " << result[0] << " and "
<< result[1] << endl;
cout << "distance: " << minum << endl;
system("pause");
return 0;
} </endl;></endl;></point></yvec.size();></point></point></point></cnt;></t></t></class></t></class></t></class></t></class></cmath></algorithm></vector></iostream>
運行結果: