一、概述
在Map的實現中,除了我們最常見的KEY值無序的HashMap之外,還有KEY有序的Map,比較常用的有兩類,一類是按KEY值的大小有序的Map,這方面的代表是TreeMap,另外一種就保持了插入順序的Map,這類的代表是LinkedHashMap. 本文介紹TreeMap.
Java提供了兩種可以用來排序的接口,分別是Comparable和Comparactor, 兩者分別說明如下:
1. Comparable
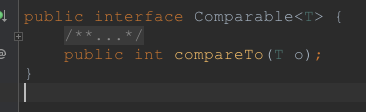
目前這是一個泛型接口,只有一個方法compareTo, 參與比較的類需要實現這個接口,這樣該類便具備了可比較性,該方法的參數表示用來比較的對象。根據這個接口的返回值是 > 0, 小於0還是等於0決定了兩個比較對象之間的大小關系。
如果一個類實現了這個接口,則該類的所有對象都是可比較的,也就是說,自身具備了比較的能力。JDK中的自帶的一些類,比如Integer, Long等都具備比較的能力,原因就是它們實現了這個接口。
這種方式適合那些比較功能是類的特點之一的類,比如前面說到的Integer.
2. Comparator
除了Comparable,JDK還提供了一個接口用來比較,這就是Comparator,其接口定義如下:
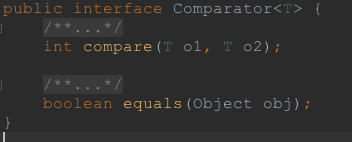
定義了兩個方法,其中equals方法可以理解為是Object.equals的增加版本,功能和equal類似,用於比較的方法是compare, 其接收兩個參數,這兩個參數不需要實現任何接口,本方法負責根據一定的規則來比較兩個對象的大小。
打個比較,這個接口的實現者好比是裁判,兩個待比較的對象找它來比較大小,它根據自己定義的規則,結合兩個對象的自身的數據,通過計算得出一個值,從而來決定哪個對象大哪個對象小。其本身並不參與比較。
有的時候待比較的對象並不需要具備可比較性,只是在某些場合下需要對它們的一個序列進行比較,或者說,可能會按多種規則對同一組序列進行比較,這個時候,用comparator構造構建器就非常合適,首先它不會侵入原類,另外,多種規則就是多個比較器,非常方便。
在JAVA裡有關比較的下操作中,如集合排序等都提供了這兩種方式的比較,我們可以根據情況進行選擇。
二、實現原理分析
顧名思議,TreeMap的實現是基於Tree的數據結構,JAVA中可以用來排序的Tree,最有名的莫過於紅黑樹,而TreeMap的實現也正是基於紅黑樹,為了更好的理解紅黑樹,前面我們已經分了兩篇來詳細說明紅黑樹,在此不再細說。本文主要從各個方面分析TreeMap的構建和使用。
1. 創建
創建一個TreeMap,總共有四種方式,如下:
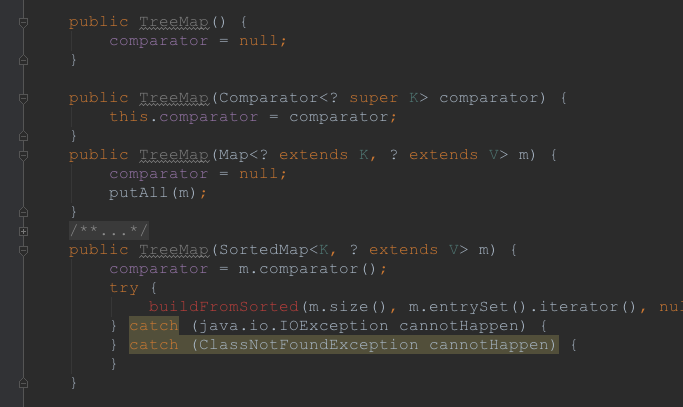
我們可以看到,TreeMap的這四種方式中其實主要分了兩種,一是comparator為null的,一種是不為null的,作為一個有序的Map,如果comparator不為NULL,則自然是使用這個來比較,否則,KEY應該繼承Comparable接口,這個也是前面解釋過的。
作為一個紅黑樹,那麼整個數據的存儲則必是一顆樹,TreeMap的實現也遵守了這一點,我們可以看一下對於樹的構造。
首先,有一個表示根節點的變量。

其次,我們看一下節點的定義,也具備紅黑樹節點的性質
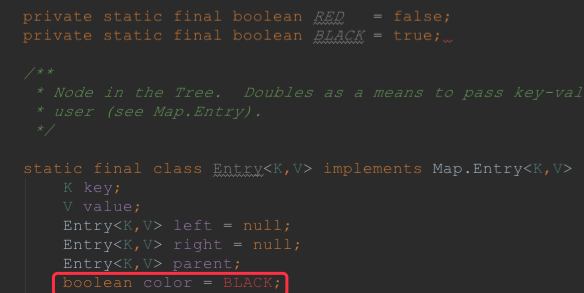
可以看到節點的定義中除了有key和value之外,還有左孩子,右孩子,父節點,以及節點的顏色,根據這三個屬性,我們可以很方便的從任何一個節點向上一級或者向下一級導航。通過對節點設置顏色,很容易實現紅黑樹的相關算法。
2. 添加
添加指添加一個新節點到樹的合適位置。那麼這個分類兩個部分,首先是要找到合適的節點,這個可以通過二叉樹的查找算法來完成,查找之後有兩個結果,如果找到相同的KEY了,則做更新操作,如果沒有找到,則需要把節點和原來的樹關聯,關聯之後,由於可能會破壞紅黑樹的性質,所以還要根據情況再做一次調整。
具體的算法如下:
1 public V put(K key, V value) {
2 Entry<K,V> t = root;
3 if (t == null) {
4 compare(key, key); // type (and possibly null) check
5
6 root = new Entry<>(key, value, null);
7 size = 1;
8 modCount++;
9 return null;
10 }
11 int cmp;
12 Entry<K,V> parent;
13 // split comparator and comparable paths
14 Comparator<? super K> cpr = comparator;
15 if (cpr != null) {
16 do {
17 parent = t;
18 cmp = cpr.compare(key, t.key);
19 if (cmp < 0)
20 t = t.left;
21 else if (cmp > 0)
22 t = t.right;
23 else
24 return t.setValue(value);
25 } while (t != null);
26 }
27 else {
28 if (key == null)
29 throw new NullPointerException();
30 Comparable<? super K> k = (Comparable<? super K>) key;
31 do {
32 parent = t;
33 cmp = k.compareTo(t.key);
34 if (cmp < 0)
35 t = t.left;
36 else if (cmp > 0)
37 t = t.right;
38 else
39 return t.setValue(value);
40 } while (t != null);
41 }
42 Entry<K,V> e = new Entry<>(key, value, parent);
43 if (cmp < 0)
44 parent.left = e;
45 else
46 parent.right = e;
47 fixAfterInsertion(e);
48 size++;
49 modCount++;
50 return null;
51 }
上面的代碼就是整個添加的過程,關鍵的地方進行了加粗顯示,可以看到,在查找的時候,實現時根據比較器是否存在來決定采用哪一種方式進行比較,如果比較之後沒有找到對應的節點,則parent變量記錄了最後一個不為葉子節點的節點,該節點即為新節點的父節點。新增後,需要對樹重新做調整。
調整算法已經在紅黑樹部分介紹過了,所以這裡就不再細說。
3. 刪除
刪除的話同樣也是先通過二叉樹的查找算法找到對應的節點,如果節點有兩個孩子節點,則需要進一步查找其直接後繼,然後針對其後繼節點做刪除操作。這樣可以保證被刪除的元素只有最多不超過一個節點。
刪除完成後,根據被刪除節點的後繼節點的情況做相應的刪除修復操作,以保證刪除後,原樹還是一個紅黑樹,刪除的完整代碼如下:
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
// Fix replacement
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;
} else { // No children. Use self as phantom replacement and unlink.
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
修復的操作在前面的紅黑樹中已經介紹了,就不再詳細分析了。
4. 遍歷操作
和普通的Map相比,作為一個排序Map,TreeMap也提供了各種遍歷的操作,如headMap, tailMap,descendingMap等,我們可以方便的進行正序或倒序的遍歷,這得益於節點的雙向關聯。在此不再一一描述
三、總結
至此,基於紅黑數的TreeMap就算是完全分析完了,這是一種很經典的實現,通過對其源碼的分析我們可以更深刻的理解紅黑樹,也可以學習到一些好的設計思想。同時,也有助於我們正確地使用紅黑樹