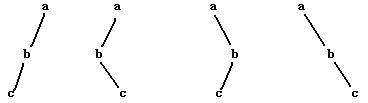
我們都很熟悉二叉樹的前序、中序、後序遍歷,在數據結構中常提出這樣的問題:已知一棵二叉樹的前序和中序遍歷,求它的後序遍歷,相應的,已知一棵二叉樹的後序遍歷和中序遍歷序列你也能求出它的前序遍歷。然而給定一棵二叉樹的前序和後序,你卻不能確定其中序遍歷序列,考慮如下圖中的幾棵二叉樹:
所有這些二叉樹都有著相同的前序遍歷和後序遍歷,但中序遍歷卻不相同。
 輸入描述 Input Description
輸入描述 Input Description
輸入文件共2行,第一行表示該樹的前序遍歷結果,第二行表示該樹的後序遍歷結果。輸入的字符集合為{a-z},長度不超過26。
輸出描述 Output Description輸出文件只包含一個不超過長整型的整數,表示可能的中序遍歷序列的總數。
樣例輸入 Sample Inputabc
cba
樣例輸出 Sample Output4
只有一個兒子 的節點 才會在知道 前序後序 的情況下有不同的中序遍歷,所以將題目轉化成找 只有一個兒子的節點個數。
可以很容易的找出這類節點在前序後序中出現的規律。(前序中出現AB,後序中出現BA,則這個節點只有一個兒子)
每個這類節點有兩種中序遍歷(及兒子在左,兒子在右)根據乘法原理中序遍歷數為 2^節點個數 種
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
char qian[30];
char hou[30];
int ans=0;
int main()
{
scanf("%s%s",qian,hou);
for(int i=0;i<=strlen(qian)-1;i++)
for(int j=1;j<=strlen(hou)-1;j++)
if(qian[i]==hou[j]&&qian[i+1]==hou[j-1])
ans++;
printf("%d",1<<ans);
}
時間限制: 1 s 空間限制: 64000 KB 題目等級 : 白銀 Silver 題目描述 Description
輸入一棵二叉樹的先序和中序遍歷序列,輸出其後序遍歷序列。
輸入描述 Input Description
共兩行,第一行一個字符串,表示樹的先序遍歷,第二行一個字符串,表示樹的中序遍歷。
輸出描述 Output Description僅一行,表示樹的後序遍歷序列。
樣例輸入 Sample Inputabdehicfg
dbheiafcg
樣例輸出 Sample Outputdhiebfgca
數據范圍及提示 Data Size & Hint輸入長度不大於255。
代碼
#include<iostream>
using namespace std;
int len;
string s1,s2;
void dfs(int s,int l,int r)
{
if(l==r)return;
int pos=l;
for(int i=l;i<=r;i++)if(s1[s]==s2[i]){pos=i;break;}
dfs(s+1,l,pos);
dfs(s+pos-l+1,pos+1,r);
cout<<s1[s];
}
int main()
{
cin>>s1>>s2;
len=s1.length();
dfs(0,0,len);
}
時間限制: 1 s 空間限制: 32000 KB 題目等級 : 白銀 Silver 題目描述 Description
求一棵二叉樹的前序遍歷,中序遍歷和後序遍歷
輸入描述 Input Description第一行一個整數n,表示這棵樹的節點個數。
接下來n行每行2個整數L和R。第i行的兩個整數Li和Ri代表編號為i的節點的左兒子編號和右兒子編號。
輸出描述 Output Description輸出一共三行,分別為前序遍歷,中序遍歷和後序遍歷。編號之間用空格隔開。
樣例輸入 Sample Input5
2 3
4 5
0 0
0 0
0 0
樣例輸出 Sample Output1 2 4 5 3
4 2 5 1 3
4 5 2 3 1
數據范圍及提示 Data Size & Hintn <= 16
代碼
#include<iostream>
using namespace std;
int n;
struct node{
int l,r;
}tree[20];
void dfs(int v)
{
cout<<v<<' ';
if(tree[v].l!=0)dfs(tree[v].l);
if(tree[v].r!=0)dfs(tree[v].r);
}
void afs(int v)
{
if(tree[v].l!=0)afs(tree[v].l);
cout<<v<<' ';
if(tree[v].r!=0)afs(tree[v].r);
}
void cfs(int v)
{
if(tree[v].l!=0)cfs(tree[v].l);
if(tree[v].r!=0)cfs(tree[v].r);
cout<<v<<' ';
}
int main()
{
cin>>n;
int x,y;
for(int i=1;i<=n;i++)
{
cin>>x>>y;
tree[i].l=x;
tree[i].r=y;
}
dfs(1);cout<<endl;
afs(1);cout<<endl;
cfs(1);
}