防線修建(1s 512MB)defense
【問題描述】
近來A國和B國的矛盾激化,為了預防不測,A國准備修建一條長長的防線,當然修建防線的話,肯定要把需要保護的城市修在防線內部了。可是A國上層現在還猶豫不決,到底該把哪些城市作為保護對象呢?又由於A國的經費有限,所以希望你能幫忙完成如下的一個任務:
1.給出你所有的A國城市坐標
2.A國上層經過討論,考慮到經濟問題,決定取消對i城市的保護,也就是說i城市不需要在防線內了
3.A國上層詢問對於剩下要保護的城市,修建防線的總經費最少是多少
你需要對每次詢問作出回答。注意單位1長度的防線花費為1。
A國的地形是這樣的,形如下圖,x軸是一條河流,相當於一條天然防線,不需要你再修建
A國總是有兩個城市在河邊,一個點是(0,0),一個點是(n,0),其余所有點的橫坐標均大於0小於n,縱坐標均大於0。A國有一個不在(0,0)和(n,0)的首都。
(0,0),(n,0)和首都這三個城市是一定需要保護的。
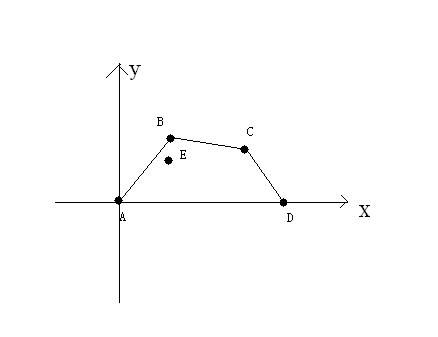
上圖中,A,B,C,D,E點為A國城市,且目前都要保護,那麼修建的防線就會是A-B-C-D,花費也就是線段AB的長度+線段BC的長度+線段CD的長度
如果,這個時候撤銷B點的保護,那麼防線變成下圖
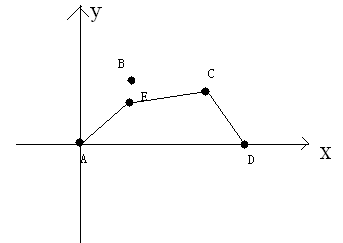
【輸入格式】
第一行,三個整數n,x,y分別表示河邊城市和首都是(0,0),(n,0),(x,y)。
第二行,一個整數m。
接下來m行,每行兩個整數a,b表示A國的一個非首都非河邊城市的坐標為(a,b)。
再接下來一個整數q,表示修改和詢問總數。
接下來q行每行要麼形如1 i,要麼形如2,分別表示撤銷第i個城市的保護和詢問。
【輸出格式】
對於每個詢問輸出1行,一個實數v,表示修建防線的花費,保留兩位小數
【樣例輸入】
4 2 1
2
1 2
3 2
5
2
1 1
2
1 2
2
【樣例輸出】
6.47
5.84
4.47
【數據范圍】
30%的數據m<=1000,q<=1000
100%的數據m<=100000,q<=200000,n>1
所有點的坐標范圍均在10000以內, 數據保證沒有重點
題解:
主要算法:Set;計算幾何;快速排序;
題意即為支持刪點維護一個上凸殼
由於只需要支持刪點的操作
那麼離線倒序處理,就變為加點操作
若要加入的點在凸包內,那就把它丟掉······
如果這個點在凸包外
分別考慮這個點左右兩邊的點
向兩個方向維護上凸殼
這個過程用set實現
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdlib>
5 #include<cstdio>
6 #include<cmath>
7 #include<set>
8 using namespace std;
9 inline int Get()
10 {
11 int x = 0;
12 char c = getchar();
13 while('0' > c || c > '9') c = getchar();
14 while('0' <= c && c <= '9')
15 {
16 x = (x << 3) + (x << 1) + c - '0';
17 c = getchar();
18 }
19 return x;
20 }
21 const int me = 200233;
22 int n, m, x, y, e;
23 int nu;
24 double sum;
25 struct dot
26 {
27 int x, y;
28 inline bool operator < (const dot &z) const
29 {
30 if(x != z.x) return x < z.x;
31 return y < z.y;
32 }
33 };
34 dot o;
35 dot a[me];
36 int flag[me];
37 bool vis[me];
38 int num[me];
39 double ans[me];
40 multiset<dot> c;
41 inline double Dis(const int &ax, const int &ay, const int &bx, const int &by)
42 {
43 return sqrt((ax - bx) * (ax - bx) + (ay - by) * (ay - by));
44 }
45 inline int Cross(const int &ax, const int &ay, const int &bx, const int &by)
46 {
47 return ax * by - bx * ay;
48 }
49 inline void Add(dot v)
50 {
51 multiset<dot>::iterator l = c.upper_bound(v), r = l;
52 --l;
53 if(Cross((r -> x) - (l -> x), (r -> y) - (l -> y), v.x - (l -> x), v.y - (l -> y)) <= 0) return;
54 sum -= Dis((l -> x), (l -> y), (r -> x), (r -> y));
55 multiset<dot>::iterator now;
56 while(l != c.begin())
57 {
58 now = l;
59 --l;
60 if(Cross(v.x - (l -> x), v.y - (l -> y), (now -> x) - (l -> x), (now -> y) - (l -> y)) >= 0)
61 {
62 ++l;
63 break;
64 }
65 sum -= Dis((now -> x), (now -> y), (l -> x), (l -> y));
66 c.erase(now);
67 }
68 while(true)
69 {
70 now = r;
71 ++r;
72 if(r == c.end())
73 {
74 --r;
75 break;
76 }
77 if(Cross(v.x - (r -> x), v.y - (r -> y), (now -> x) - (r -> x), (now -> y) - (r -> y)) <= 0)
78 {
79 --r;
80 break;
81 }
82 sum -= Dis((now -> x), (now -> y), (r -> x), (r -> y));
83 c.erase(now);
84 }
85 c.insert(v);
86 sum += Dis((l -> x), (l -> y), v.x, v.y) + Dis(v.x, v.y, (r -> x), (r -> y));
87 }
88 int main()
89 {
90 o.x = o.y = 0;
91 c.insert(o);
92 o.x = n = Get();
93 c.insert(o);
94 o.x = x = Get();
95 o.y = y = Get();
96 c.insert(o);
97 m = Get();
98 sum = Dis(0, 0, x, y) + Dis(x, y, n, 0);
99 for(int i = 1; i <= m; ++i)
100 {
101 a[i].x = Get();
102 a[i].y = Get();
103 }
104 e = Get();
105 for(int i = 1; i <= e; ++i)
106 {
107 flag[i] = Get();
108 if(flag[i] == 1)
109 {
110 num[i] = Get();
111 vis[num[i]] = true;
112 }
113 }
114 for(int i = 1; i <= m; ++i)
115 if(!vis[i])
116 Add(a[i]);
117 for(int i = e; i >= 1; --i)
118 {
119 if(flag[i] == 1) Add(a[num[i]]);
120 else ans[++nu] = sum;
121 }
122 for(int i = nu; i >= 1; --i)
123 printf("%.2lf\n", ans[i]);
124 }