tarjan講解（用codevs1332（tarjan的裸題）講解），tarjancodevs1332

tarjan講解（用codevs1332（tarjan的裸題）講解），tarjancodevs1332

主要借助這道比較裸的題來講一下tarjan這種算法

 tarjan是一種求解有向圖強連通分量的線性時間的算法。（用dfs來實現）

如果兩個頂點可以相互通達，則稱兩個頂點強連通。如果有向圖G的每兩個頂點都強連通，稱G是一個強連通圖。有向圖的極大強連通子圖，稱為強連通分量。

 

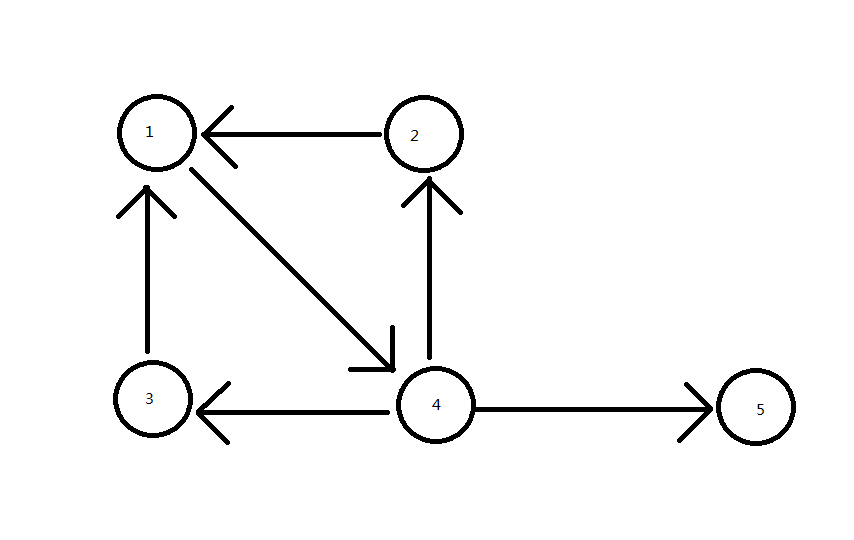
在上面這張有向圖中1，2，3，4形成了一個強連通分量，而1,2,4,和1,3,4並不是（因為它們並不是極大強連通子圖）。

tarjan是用dfs來實現的（用了tarjan後我們就可以對圖進行縮點(當然這道裸題用不到)）

這道題只要找到最大的強連通分量，並且把將該強連通分量的序號從小到大輸出（如果有一樣大的強連通分量，那麼輸出含有更小的點的那一個）

下面來道題：（tarjan代碼加注釋往下拉）

題目

題目描述 Description 在幻想鄉，上白澤慧音是以知識淵博聞名的老師。春雪異變導致人間之裡的很多道路都被大雪堵塞，使有的學生不能順利地到達慧音所在的村莊。因此慧音決定換一個能夠聚集最多人數的村莊作為新的教學地點。人間之裡由N個村莊（編號為1..N）和M條道路組成，道路分為兩種一種為單向通行的，一種為雙向通行的，分別用1和2來標記。如果存在由村莊A到達村莊B的通路，那麼我們認為可以從村莊A到達村莊B，記為(A,B)。當(A,B)和(B,A)同時滿足時，我們認為A,B是絕對連通的，記為<A,B>。絕對連通區域是指一個村莊的集合，在這個集合中任意兩個村莊X,Y都滿足<X,Y>。現在你的任務是，找出最大的絕對連通區域，並將這個絕對連通區域的村莊按編號依次輸出。若存在兩個最大的，輸出字典序最小的，比如當存在1,3,4和2,5,6這兩個最大連通區域時，輸出的是1,3,4。 輸入描述 Input Description 第1行：兩個正整數N,M 第2..M+1行：每行三個正整數a,b,t, t = 1表示存在從村莊a到b的單向道路，t = 2表示村莊a,b之間存在雙向通行的道路。保證每條道路只出現一次。 輸出描述 Output Description 第1行： 1個整數，表示最大的絕對連通區域包含的村莊個數。 第2行：若干個整數，依次輸出最大的絕對連通區域所包含的村莊編號。 樣例輸入 Sample Input 5 5 1 2 1 1 3 2 2 4 2 5 1 2 3 5 1 樣例輸出 Sample Output 3 1 3 5 數據范圍及提示 Data Size & Hint 對於60%的數據：N <= 200且M <= 10,000 對於100%的數據：N <= 5,000且M <= 50,000 View Code

 很明顯這道題需要用到tarjan

#include<stdio.h>
#include<algorithm>
using namespace std;
int dfn[500000], low[500000], stack[900000], j, number, n, m, x, y, w, hh[600000], cnt, top, c, q, ans, yy[100000];
int color[400000], u, num, p[400000];
bool d[500000];
struct node
{
    int next, z, e;
} b[110000];
void add(int aa, int bb)//鄰接表
{
    b[++cnt].e = bb;
    b[cnt].next = hh[aa];
    hh[aa] = cnt;
}

 

tarjan代碼：

int tarjan(int k)
{
    int i;
    dfn[k] = low[k] = ++number;//dfn記錄的是訪問此節點的真實時間，low記錄的是
    stack[++top] = k;將當前點入棧
    d[k] = true;//這是表示點k的狀態
    for(i = hh[k]; i != 0; i = b[i].next)
    {
        if(!dfn[b[i].e])如果當前節點沒有訪問過就繼續搜
        {
            tarjan(b[i].e);
            low[k] = min(low[k], low[b[i].e]);
        }
        else if(d[b[i].e] == true)
        {
            low[k] = min(low[k], dfn[b[i].e]);
            //當然也可以寫成low[k]=min(low[k],low[b[i].e]);
        }
    }
    if(dfn[k] == low[k])//如果該點是強連通分量的根，也就是說我們已經找到了一個強連通分量，就開始彈棧
    {
        color[k] = ++num;//把該強連通分量上的點全部染成同一種顏色
        while(1)
        {
            p[num]++;//記錄該強連通分量上的點
            d[stack[top]] = false;//棧頂元素出棧
            color[stack[top--]] = num;將棧頂元素的顏色染成當前該強連通分量的顏色
            if(stack[top + 1] == k)break;//因為根肯定是當前強連通分量上最先訪問，也就是最先入站的，所以彈出了根代表該強連通分量上的已全部彈出
        }
    }
    return 0;
}

 

int main()
{
    int i;
    scanf("%d %d", &n, &m);
    u = 1;
    for(i = 1; i <= m; i++)
    {
        scanf("%d %d %d", &x, &y, &w);
        if(w == 1)add(x, y);//建邊
        else
        {
            add(x, y);
            add(y, x);
        }
    }
    for(j = 1; j <= n; j++)
    {
        if(!dfn[j])tarjan(j);//如果當前點沒有被搜過，就從當前點進行深搜
    }
    for(i = 1; i <= n; i++)
    {
        if(p[color[i]] > ans)ans = p[color[i]], u = i;
    }
    printf("%d\n", ans);
    for(i = 1; i <= n; i++)
    {
        if(color[i] == color[u])printf("%d ", i);
    }
    return 0;
}