給一個n個點的圖和一個n個點的樹,求圖和樹上的點一一對應的方案數。(N<=17)
思路:
1.在樹的結構上進行tree DP,f[i][j]表示樹上點 i 對應圖上點 j 時,這個點所在子樹的方案數。O(n^3)。
2.我們可以發現如果按這個定義進行DP,“一一對應”的關系挺難保證。若枚舉出全排列得到對應關系,這樣就C(n,n)=n! 只能拿到暴力分;那麼我們就不限制“一一對應”而改為“一對多”的關系進行tree DP,利用容斥原理達到O(2^n)的復雜度。(P.S.至於為什麼用容斥原理我也不清楚,待我弄懂之後我會再更新的。)
3.這題的容斥原理應用是這樣的:用二進制數枚舉出每次DP有哪些數沒有對應的樹上的點,將所有情況下的DP方案數之和按求補集的公式來求就是“所有數都一一對應樹上的點”的答案。
下圖中圓圈1表示數1沒有對應的點的方案數,依次類推。有顏色部分是我們要求的補集。
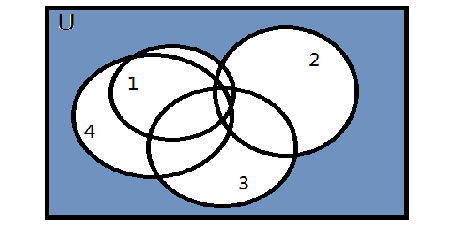
下面附上代碼——
1 #include<cstdio>
2 #include<cstdlib>
3 #include<cstring>
4 #include<iostream>
5 using namespace std;
6
7 typedef long long LL;
8 const int N=20,M=400;
9 struct node{int x,y,next;}a[2*N];
10 int last[N],len;
11 bool v[N][N],vis[N];
12 LL f[N][N];
13 int b[N],bt;
14
15 void add(int x,int y)
16 {
17 len++;
18 a[len].x=x,a[len].y=y;
19 a[len].next=last[x],last[x]=len;
20 }
21
22 void dfs(int x,int fa)
23 {
24 /*for(int k=last[x];k;k=a[k].next)
25 {
26 int y=a[k].y;
27 if(y==fa)continue;
28 dfs(y,x);
29 }
30 for (int kk=1;kk<=bt;kk++)
31 {
32 int i=b[kk];
33 f[x][i]=1;
34 for (int k=last[x];k;k=a[k].next)
35 {
36 int y=a[k].y;
37 if (y==fa) continue;
38 LL h=0;
39 for (int kkk=1;kkk<=bt;kkk++)
40 {
41 int j=b[kkk];
42 if (v[i][j]) h+=f[y][j];
43 }
44 f[x][i]*=h;
45 }
46 }*///邊建樹,邊不重復地DP
47 if (vis[x]) return;
48 for (int kk=1;kk<=bt;kk++)
49 {
50 int i=b[kk];
51 f[x][i]=1;
52 for (int k=last[x];k;k=a[k].next)
53 {
54 int y=a[k].y;
55 if (y==fa) continue;
56 dfs(y,x);
57 vis[y]=true;
58 LL h=0;
59 for (int kkk=1;kkk<=bt;kkk++)
60 {
61 int j=b[kkk];
62 if (v[i][j]) h+=f[y][j];
63 }
64 f[x][i]*=h;
65 }
66 }//打標記,快一點
67 }
68
69 int main()
70 {
71 int n,m;
72 scanf("%d%d",&n,&m);
73 memset(v,false,sizeof(v));
74 for (int i=1;i<=m;i++)
75 {
76 int x,y;
77 scanf("%d%d",&x,&y);
78 v[x][y]=v[y][x]=true;
79 }
80 memset(last,0,sizeof(last));
81 len=0;
82 for (int i=1;i<n;i++)
83 {
84 int x,y;
85 scanf("%d%d",&x,&y);
86 add(x,y),add(y,x);
87 }
88 LL ans=0;
89 for (int i=1;i<(1<<n);i++)
90 {
91 bt=0;
92 for (int j=1;j<=n;j++)
93 if (i&(1<<(j-1))) b[++bt]=j;
94 memset(vis,false,sizeof(vis));
95 dfs(1,0);
96 LL h=0;
97 for (int j=1;j<=bt;j++)
98 h+=f[1][b[j]];
99 if ((n-bt)%2==0) ans+=h;//按補集
100 else ans-=h;
101 }
102 printf("%lld\n",ans);
103 return 0;
104 }