時間限制: 1 s 空間限制: 128000 KB 題目等級 : 鑽石 Diamond 題目描述 Description
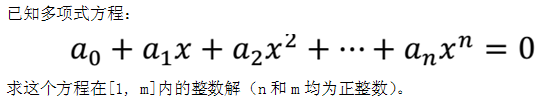
輸入文件名為equation.in。
輸入共n+2行。
第一行包含2個整數n、m,每兩個整數之間用一個空格隔開。
接下來的n+1行每行包含一個整數,依次為a0,a1,a2,……,an。
輸出描述 Output Description
輸出文件名為equation.out。
第一行輸出方程在[1, m]內的整數解的個數。
接下來每行一個整數,按照從小到大的順序依次輸出方程在[1, m]內的一個整數解。
樣例輸入 Sample Input
equation.in
equation.out
2 10
1
-2
1
1
1
equation.in
equation.out
2 10
2
-3
1
2
1
2
樣例輸出 Sample Output
equation.in
equation.out
2 10
1
3
2
0
數據范圍及提示 Data Size & Hint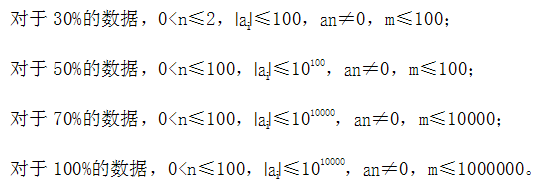
1 /*
2 嗯rp很重要.(RP++).
3 這題是要求[1,m]區間中的合法解.
4 然而m是一個非常大的數.
5 不考慮精度問題枚舉的話o(nm)應該是可行的
6 (FFT壓位我真是太機智了哈哈哈哈哈哈哈)
7 (畫外音:10^10000壓位+處理應該會T吧orz)
8 so我們考慮這個方程在剩余系意義下的解.
9 (ax)%p等價於(ax+p)%p.
10 我們mod兩個prime.
11 因為mod一個prime的解可能不充分.
12 最後從[1,m]中掃一遍合法解.
13 */
14 #include<iostream>
15 #include<cstring>
16 #include<cstdio>
17 #define MAXN 201
18 #define MAXM 1000001
19 #define LL long long
20 using namespace std;
21 int n,m,ans,p[4];
22 LL a[3][MAXM];
23 bool b[MAXM];
24 char s1[MAXM];
25 void slove1(char s[],int l,int k)
26 {
27 bool flag=false;
28 int x;
29 for(int i=1;i<=2;i++)
30 {
31 x=0;
32 if(s[0]=='-') x=1,flag=true;
33 while(x<l) a[i][k]=(a[i][k]*10%p[i]+s[x]-48)%p[i],x++;
34 if(flag) a[i][k]=p[i]-a[i][k];//負數.
35 }
36 }
37 bool check(int x,int k)
38 {
39 LL tot=0,w=1;
40 for(int i=0;i<=n;i++)
41 tot=(tot+a[k][i]*w%p[k])%p[k],w=(w*x)%p[k];
42 return tot%p[k];
43 }
44 void slove()
45 {
46 for(int i=1;i<=p[1];i++)
47 {
48 if(check(i,1)) continue;
49 for(int j=i;j<=m;j+=p[1])
50 if(!check(j,2)) b[j]=true;
51 }
52 int tot=0;
53 for(int i=1;i<=m;i++)
54 if(b[i]) tot++;
55 printf("%d\n",tot);
56 for(int i=1;i<=m;i++)
57 if(b[i]) printf("%d\n",i);
58 }
59 int main()
60 {
61 p[1]=22861,p[2]=1000007977;
62 scanf("%d%d",&n,&m);
63 for(int i=0;i<=n;i++)
64 {
65 cin>>s1;
66 int l=strlen(s1);
67 slove1(s1,l,i);
68 }
69 slove();
70 return 0;
71 }