一、題目背景
給定一個二叉樹的前序和中序遍歷,求出它的後序遍歷
二叉樹的遍歷可參考
http://blog.csdn.net/fansongy/article/details/6798278/
二、算法分析
例如下面這個二叉樹
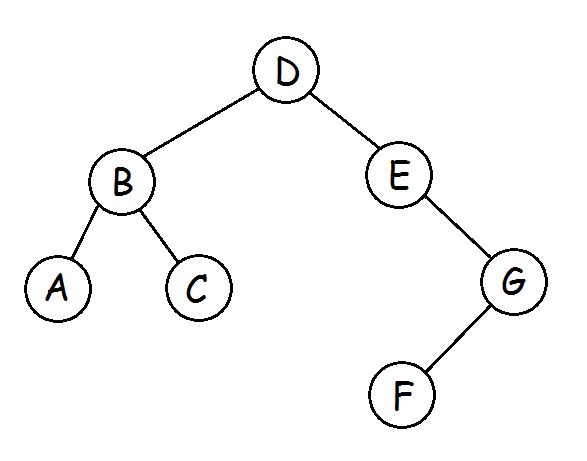
它的先序遍歷為:DBACEGF
它的中序遍歷為:ABCDEFG
它的後序遍歷為:ACBFGED
先用一個指針指向先序遍歷第一個字符,即樹的根節點D
然後在中序遍歷找到D,將此遍歷劃分為ABC和EFG,因為中序遍歷按照左中右的結構,可知在D左邊為其左子樹,右邊為其右子樹
進入其左子樹ABC,此時指針+1,指向B
在左子樹ABC中找到B,將其劃分為A和C兩部分,A為其左子樹,C為其右子樹
指針相應+2
這樣不斷遞歸下去,直到找完所有節點
整體思想就是從先序遍歷找到子樹的根節點,然後在中序遍歷左右分別遞歸,同時每加入一個節點就需給先序遍歷的指針+1,可以證明這種方法是正確的
如果需要判斷是否能夠構成二叉樹,只需在尋找根節點的時候判斷能否找到即可,若不能找到則說明不能構成二叉樹
1 #include <algorithm>
2 #include <iostream>
3 #include <cstdlib>
4 #include <cstring>
5 #include <cstdio>
6 #include <cmath>
7 #define N 10000
8 using namespace std;
9
10 char mid[N],frt[N];
11 int k,cr[N],cl[N];
12 int bt(int l,int r)
13 {
14 if (l>r) return -1;
15 if (l==r)
16 {
17 k++;
18 return l;
19 }
20 int i;
21 for (i=l;i<=r;i++)
22 {
23 if (frt[k]==mid[i])
24 {
25 break;
26 }
27 }
28 k++;
29 cl[i]=bt(l,i-1);
30 cr[i]=bt(i+1,r);
31 return i;
32 }
33 void outp(int x)
34 {
35 if (x==-1) return;
36 outp(cl[x]);
37 outp(cr[x]);
38 cout<<mid[x];
39 }
40 int main()
41 {
42 int len,i;
43 freopen("bt.in","r",stdin);
44 freopen("bt.out","w",stdout);
45 gets(frt);
46 gets(mid);
47 k=0;
48 len=strlen(mid);
49 for (i=0;i<=len;i++) cl[i]=cr[i]=-1;
50 outp(bt(0,len-1));
51 cout<<endl;
52 return 0;
53 }
三、題目來源
九度Oline Judge 題目1385:重建二叉樹 (這個需要判斷是否能夠建成)
http://ac.jobdu.com/problem.php?pid=1385
南陽理工學院在線評測系統 題目756:重建二叉樹 (這個是輸入中序和後序遍歷,求出先序遍歷)
http://acm.nyist.net/JudgeOnline/problem.php?pid=756
版權所有,轉載請聯系作者,違者必究
QQ:740929894