筆試題31. LeetCode OJ (18)

筆試題31. LeetCode OJ (18)

如果說求兩個數相加是輕松，那麼求三個數相加則是痛苦，如果說求四個數相加呢-----絕望。

沒錯，拿到這個題的時候確實有些絕望，但是既然開發這個題的人如此刁難我們，我們也不能放棄，不要辜負別人的一番好意，所以我咬牙繼續。

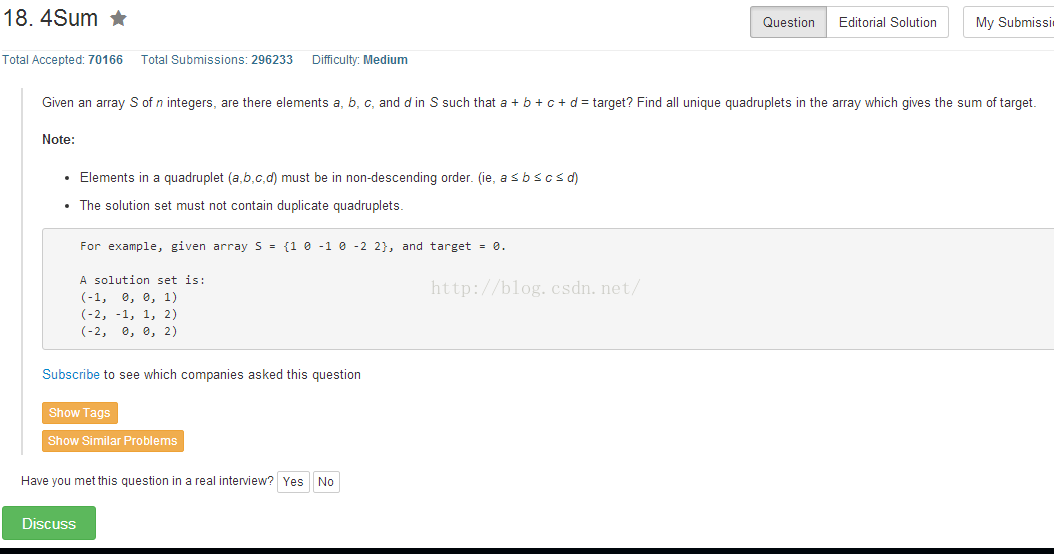
經歷過前面的風雨，我們也學會了成長，這道題是建立在前面的題的基礎上而開始的。題目的要求比較嚴格，要求四個數的和和target的值相等，且四個數字不重復且升序。

所以我們得一個一個的去試探，也就是遍歷，這個應該得循環嵌套的遍歷，因為我們不能放過每一種情況，因為它可能在包含在我們要求的情況中。思路其實不難，代碼如下：

class Solution {
public:
	vector> fourSum(vector& nums, int target) {
		vector > last;
		int len = nums.size();
		if (len < 4)
		{
			return last;
		}
		//1.排序
		sort(nums.begin(), nums.end());
		//遍歷
		//特殊處理一下，若最小的四個數的和比target還大或者最大的四個數的和比target還大，那麼我們直接退出
		if (nums[len - 1] + nums[len - 2] + nums[len - 3] + nums[len - 4] < target)
		{
			return last;
		}
		if (nums[0] + nums[1] + nums[2] + nums[3] > target)
		{
			return last;
		}
        //循環遍歷，不能重復，那麼必須得一個一個的試，因為排序了，所以情況的復雜性減少了很多
		for (int i = 0; i < len - 3; ++i)
		{ //1層
			while (i > 0 && nums[i] == nums[i - 1])
			{//處理重復數字，但是第一次遍歷到的時候不能處理掉，否則可能錯過一些解
				++i;
			}
			for (int j = i + 1; j i + 1 && nums[j] == nums[j - 1])
				{//處理重復數字，但是第一次遍歷到的時候不能處理掉，否則可能錯過一些解
					++j;
				}
				int pos1 = j + 1;
				while (pos1 < len - 1)
				{ //3層
					while (pos1>j + 1 && nums[pos1] == nums[pos1 - 1])
					{//處理重復數字，但是第一次遍歷到的時候不能處理掉，否則可能錯過一些解
						++pos1;
					}
					int pos2 = pos1 + 1;
					while (pos2 < len && nums[i] + nums[j] + nums[pos1] + nums[pos2] < target)
					{
						++pos2;
					}
					if (pos2 == len)
					{
						++pos1;
						continue;
					}
					if (nums[i] + nums[j] + nums[pos1] + nums[pos2] == target)
					{
						vector tmp;
						tmp.push_back(nums[i]);
						tmp.push_back(nums[j]);
						tmp.push_back(nums[pos1]);
						tmp.push_back(nums[pos2]);
						last.push_back(tmp);
						++pos1;
						continue;
					}
					if (nums[i] + nums[j] + nums[pos1] + nums[pos2] > target)
					{//
						++pos1;
						continue;
					}
				}
			}
		}
		return last;
	}
};