Integer Partition（hdu4658）2013 Multi-University Training Contest 6 整數拆分二，excel2013拆分單元格

Integer Partition（hdu4658）2013 Multi-University Training Contest 6 整數拆分二，excel2013拆分單元格

Integer Partition

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 524 Accepted Submission(s): 238

Problem Description Given n, k, calculate the number of different (unordered) partitions of n such that no part is repeated k or more times.  

Input First line, number of test cases, T. 
Following are T lines. Each line contains two numbers, n and k. 

1<=n,k,T<=10⁵  

Output T lines, each line contains answer to the responding test case.
Since the numbers can be very large, you should output them modulo 10⁹+7.  

Sample Input 4 4 2 4 3 4 4 4 5  

Sample Output 2 4 4 5  

Source 2013 Multi-University Training Contest 6       

題目：http://acm.hdu.edu.cn/showproblem.php?pid=4658

 

題意：問一個數n能被拆分成多少種方法，且每一種方法裡數字重復個數不能超過k（等於k）。   五邊形數定理續，結合上一題（hdu4651），先打表，然後把大於k的個數剪掉；  
 
好吧，再啰嗦一遍：  

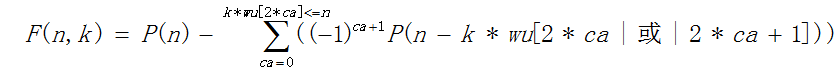
用了五邊形數定理以及生成函數，然而我看懂了生成函數怎麼搞這題卻不知道為啥生成函數是五邊形數形式= =

首先觀察下面的圖片：

很容易我們可以發現用這種方式構造N個五邊形（假設一個點也算一個五邊形），需要點的個數為： 

n∗(3n−1)2

 

---

接下來我們來看一下數拆分。 
提問：將一個正整數N拆成不少於一個數的和，問有多少種方案。

很容易我們可以構造一個多項式： 
P(x)=(1+x1+x2+...)(1+x2+x4+...)(1+x3+x6+...)... 
=Px(0)x0+Px(1)x1+Px(2)x2+...+Px(n)xn

可以發現N的數拆分的方案數正對應著多項式展開後xn的系數Px(n)

考慮如下等式： 

(1+x1+x2+...)=11−x
因此我們有： 
∏i=0∞11−xi=∑i=0∞Px(i)xi
其中上式等式左邊是歐拉函數ϕ(x)的倒數。即： 
1ϕ(x)=∑i=0∞Px(i)xi

 

歐拉函數ϕ(x)的展開式為： 

ϕ(x)=(1−x)(1−x2)(1−x3)...=1−x−x2+x5+x7−x12−x15+x22+x26−...
其中的x的指數正對應著廣義五邊形數！

 

n01-12-23-34-4… P(n) 0 1 2 5 7 12 15 22 26 …

現在我們要計算Px(n)，由於1ϕ(x)=P(x)，亦即ϕ(x)P(x)=1。

 

(1−x−x2+x5+...)(Px(0)+Px(1)x+Px(2)x2+Px(3)x3+...)=1
所以：Px(n)=Px(n−1)+Px(n−2)−Px(n−5)−Px(n−7)+...

 

由於對於滿足i(3i−1)2≤n的i的個數不超過(√n)個，於是計算所有Px(n)的復雜度為O(n(√n))

---

上面我們說明的是不帶限制的數拆分，現在我們給定一個限制：拆分出來的每種數的個數不能大於等於k（這也是本題的要求）。

類似的，我們考慮生成函數： 

(1+x1+x2+...+xk−1)(1+x2+x4+...x2(k−1))...=∏i=0∞1−xki1−xi=ϕ(xk)ϕ(x)=ϕ(xk)P(x)
展開ϕ(xk)得： 
(1−xk)(1−x2k)(1−x3k)...=1−xk−x2k+x5k+x7k−x12k−x15k+...
然後可得： 
ϕ(xk)P(x)=(1−xk−x2k+x5k...)(Px(0)+Px(1)x+Px(2)x2+Px(3)x3+...)
令Fk(n)表示n的滿足數拆分時每種數的個數小於等於k的數拆分方案數。則有： 
Fk(n)=Px(n)−Px(n−k)−Px(n−2k)+Px(n−5k)+...
  一開始超時了，不然把取余的部分修改了下就過了。。。  
  卡過啊！
  轉載請注明出處：尋找&星空の孩子

 1 #include<iostream>
 2 #include<cstdio>
 3 #define NN 100005
 4 #define LL __int64
 5 #define mod 1000000007
 6 
 7 using namespace std;
 8 LL wu[NN],pa[NN];
 9 void init()
10 {
11     pa[0]=1;
12     pa[1]=1;
13     pa[2]=2;
14     pa[3]=3;
15     LL ca=0;
16     for(LL i=1; i<=100000/2; i++)
17     {
18         wu[ca++]=i*(3*i-1)/2;
19         wu[ca++]=i*(3*i+1)/2;
20         if(wu[ca-1]>100000) break;
21     }
22     for(LL i=4; i<=100000; i++)
23     {
24         pa[i]=(pa[i-1]+pa[i-2])%mod;
25         ca=1;
26         while(wu[2*ca]<=i)
27         {
28             if(ca&1)
29             {
30                 pa[i]=(pa[i]-pa[i-wu[2*ca]]);
31                 pa[i]=(pa[i]%mod+mod)%mod;
32                 if(wu[2*ca+1]<=i)
33                     pa[i]=(pa[i]-pa[i-wu[2*ca+1]]),pa[i]=(pa[i]%mod+mod)%mod;
34             }
35             else
36             {
37                 pa[i]=(pa[i]+pa[i-wu[2*ca]]);
38                 pa[i]=(pa[i]%mod+mod)%mod;
39                 if(wu[2*ca+1]<=i)
40                     pa[i]=(pa[i]+pa[i-wu[2*ca+1]]),pa[i]=(pa[i]%mod+mod)%mod;
41             }
42             ca++;
43         }
44     }
45 }
46 LL work(int n,int k)
47 {
48     LL ans=pa[n];
49     LL ca=0;
50     while(k*wu[2*ca]<=n)
51     {
52         if(ca&1)
53         {
54             ans=(ans+pa[n-k*wu[2*ca]]);
55             ans=(ans%mod+mod)%mod;
56             if(k*wu[2*ca+1]<=n)
57                 ans=(ans+pa[n-k*wu[2*ca+1]]),ans=(ans%mod+mod)%mod;
58         }
59         else
60         {
61             ans=(ans-pa[n-k*wu[2*ca]]);
62             ans=(ans%mod+mod)%mod;
63             if(k*wu[2*ca+1]<=n)
64                 ans=(ans-pa[n-k*wu[2*ca+1]]),ans=(ans%mod+mod)%mod;
65         }
66         ca++;
67     }
68     return ans;
69 }
70 int main()
71 {
72     int T,n,k;
73     init();
74     scanf("%d",&T);
75     while(T--)
76     {
77         scanf("%d%d",&n,&k);
78         printf("%I64d\n",work(n,k));
79     }
80     return 0;
81 
82 }

 

數論還有很多需要學習！