We all know that GukiZ often plays with arrays.
Now he is thinking about this problem: how many arrays a, of length n, with non-negative elements strictly less then 2l meet the following condition: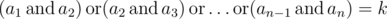 
? Here operation 
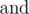means bitwise AND (in Pascal it is equivalent to and, in C/C++/Java/Python it is equivalent to &), operation 
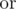means bitwise OR (in Pascal it is equivalent to 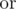, inC/C++/Java/Python it is equivalent to |).
Because the answer can be quite large, calculate it modulo m. This time GukiZ hasn't come up with solution, and needs you to help him!
InputFirst and the only line of input contains four integers n, k, l, m (2 ≤ n ≤ 1018, 0 ≤ k ≤ 1018, 0 ≤ l ≤ 64, 1 ≤ m ≤ 109 + 7).
OutputIn the single line print the number of arrays satisfying the condition above modulo m.
Sample test(s) input2 1 2 10output
3input
2 1 1 3output
1input
3 3 2 10output
9Note
In the first sample, satisfying arrays are {1, 1}, {3, 1}, {1, 3}.
In the second sample, only satisfying array is {1, 1}.
In the third sample, satisfying arrays are{0, 3, 3}, {1, 3, 2}, {1, 3, 3}, {2, 3, 1}, {2, 3, 3}, {3, 3, 0}, {3, 3, 1}, {3, 3, 2}, {3, 3, 3}.
題意：你可以任意挑選小於2^l的n個數，讓它們以這個公式
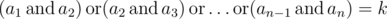，兩兩取與再取或的方式最後答案為k，問你有多少種方案數，答案取余m
思路：這題看了別人的題解之後終於明白了。首先，我們把k轉換為二進制來看，若某一位為1，則必須存在n個數中至少有相鄰的兩個數那一位都為1，若某一位為0，組必須存在n個數它們不能有相鄰的兩個數那一位都為1.這樣我們相當於求k每一位在n個數字中的方案數，答案是每一位的方案數相乘起來。
注意l=64的時候，要特別注意一下
我用了無符號的long long 各種錯。。。最後還是long long 過的。
不知道是不是我編譯器壞了。
轉載請注明出處：
尋找&星空の孩子
題目鏈接：http://codeforces.com/contest/551/problem/D
1 #include<stdio.h>
2 #include<string.h>
3 #include<algorithm>
4 #define LL long long
5 using namespace std;//unsigned
6 struct matrix
7 {
8 LL mat[2][2];
9 };
10 LL mod;
11
12 matrix multiply(matrix a,matrix b)
13 {
14 matrix c;
15 memset(c.mat,0,sizeof(c.mat));
16 for(int i=0;i<2;i++)
17 {
18 for(int j=0;j<2;j++)
19 {
20 if(a.mat[i][j]==0)continue;
21 for(int k=0;k<2;k++)
22 {
23 if(b.mat[j][k]==0)continue;
24 c.mat[i][k]+=a.mat[i][j]*b.mat[j][k]%mod;
25 // c.mat[i][k]%=mod;
26 if(c.mat[i][k]>mod) c.mat[i][k]-=mod;
27 else if(c.mat[i][k]<0) c.mat[i][k]+=mod;
28 }
29 }
30 }
31 return c;
32 }
33
34 matrix quicklymod(matrix a,LL n)
35 {
36 matrix res;
37 memset(res.mat,0,sizeof(res.mat));
38 for(int i=0;i<2;i++) res.mat[i][i]=1;
39 while(n)
40 {
41 if(n&1)
42 res=multiply(a,res);
43 a=multiply(a,a);
44 n>>=1;
45 }
46 return res;
47 }
48
49 LL ppow(LL a,LL b)
50 {
51 LL c=1;
52 while(b)
53 {
54 if(b&1) c=c*a%mod;
55 b>>=1;
56 a=a*a%mod;
57 }
58 return c;
59 }
60
61
62 int main()
63 {
64 LL n,k,l,m;
65 scanf("%I64d%I64d%I64d%I64d",&n,&k,&l,&mod);
66 if(l!=64&&k>=(unsigned long long )(1ULL<<l)){printf("0\n");return 0;}
67 matrix ans;
68 ans.mat[0][0]=1;ans.mat[0][1]=1;
69 ans.mat[1][0]=1;ans.mat[1][1]=0;
70 ans=quicklymod(ans,n);
71 //相鄰沒有連續兩個1
72 LL x=(ans.mat[0][0]+ans.mat[0][1])%mod;
73 //至少有一個連續兩個1
74 LL y=((ppow(2,n)-x)%mod+mod)%mod;
75 // printf("x=%I64d\ty=%I64d\n",x,y);
76 LL sum=1;
77 for(LL i=0;i<l;i++)
78 {
79 if(k&(1LL<<i)) sum=(sum*y)%mod;
80 else sum=sum*x%mod;
81 }
82 printf("%I64d\n",sum%mod);
83 return 0;
84 }
別人的 無符號過的。。。
