在我之前的一篇文章[ ThoughtWorks代碼挑戰——FizzBuzzWhizz游戲 通用高速版(C/C++ & C#) ]裡曾經提到過編譯器在處理被除數為常數的除法時,是有優化的,今天整理出來,一來可以了解是怎麼實現的,二來如果你哪天要寫編譯器,這個理論可以用得上。此外,也算我的一個筆記。

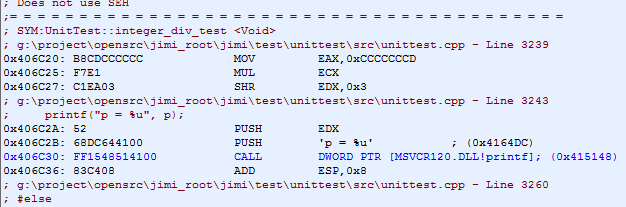
我們先來看一看編譯器優化的實例。我們所說的被除數為常數的整數除法(針對無符號整型, 有符號整型我們後面再討論),指的是,對於unsigned int a, b, c,例如:a / 10, b / 5, c / 3 諸如此類的整數除法,我們先來看看編譯器 unsigned int a, p; p = a / 10; 是如何實現的,下圖是 VS 2013 優化的結果,反匯編結果如下:
測試代碼如下:
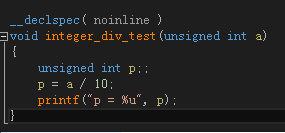
我們可以看到,編譯器並沒有編譯成整數除法DIV指令,而是先乘以一個0xCCCCCCCD(MUL指令),再把EDX右移了3位(SHR edx, 0x03),EDX的值就是我們要求的商。
其原理整理後即為:Value / 10 ~= [ [ (Value * 0xCCCCCCCD) / 2^32 ] / 2^3 ],方括號代表取整。
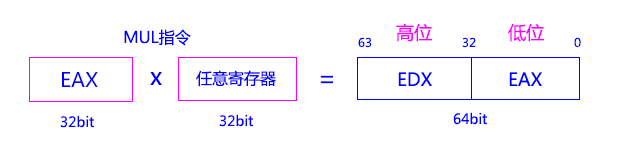
首先我們要知道一個東西,就是,Intel x86上32位無符號整型(uint32_t)相乘的結果其實是一個64位的整型,即uint64_t,相乘的結果保存在 EAX 和 EDX 兩個寄存器裡,EAX, EDX都是32位的,合在一起便是一個64位的整數了,一般記為 EDX : EAX,其中EAX是uint64_t的低位,EDX是高位。這個特性在大多數32位的CPU上都存在,即整數乘法結果的位長是被乘數位長的兩倍,當然也不排除部分CPU因為某些特殊原因,其相乘的結果依然和被乘數的位長一樣,但這樣的CPU應該很少見。只有滿足這個特性的CPU,常量的整數除法優化才能得以實現。
至於為什麼不直接使用DIV指令,原因是:即使在當今發展已經比較完善也比較流行的x86系列CPU上,整數或浮點的除法指令依然是一條比較慢的指令,CPU在整數或浮點除法一般有兩種實現方法,一種是試商法(這個非常類似人類在計算除法的過程,只不過這裡CPU使用的是二進制來試商,用條件判斷來判斷如何結束),另一種是乘以 被除數 的倒數(即 x (1.0 / 被除數)),把除法變為乘法,因為乘法在CPU裡實現是比較容易的,只需實現位移和加法器即可,並且可以並行處理。前一種方法,跟人類計算除法類似,無法做到並行處理,且計算過程是不定長的,可能很快就結束(剛好整除),可能要計算到合適的精度為止。而第二種方法,因為用無窮級數求(1.0 / 被除數)的過程涉及精度問題,這個過程花的時間也是不定長的,而且用這種方法的時候,必須把整數除法轉換為浮點除法才能進行,最後把結果再轉換為整型。而試商法可以把整除除法和浮點除法分為兩套方案,也可以合為一套方案。至於效率,第二種方法較快,但耗電會比第一種方法大,因為要用到大量的乘法器,所以x86上具體用的是那一種方法,我也不是很清楚,但是Intel手冊上寫著,Core 2架構的DIV指令的執行周期大概是13-84個周期不等。後續出的新CPU除法指令有沒有更快我不太清楚,從實現原理上,終究是沒有乘法快的,除非除法的設計有大的突破,因為Core 2上整數/浮點乘法就只需要3個時鐘周期,想接近乘法的效率是很難的,關鍵的一點就是,目前,除法指令的時鐘周期是變長的,可能很短,可能很長,平均花費的時鐘周期是乘法指令的N倍。
那麼,這麼優化的原理是什麼?怎麼得到的?可以應用於所有被除數是uint32_t的常量的整數除法嗎?答案是:可以的。但前提條件是,被除數必須是常量,如果是變量,編譯器也只能老老實實使用DIV指令。
由於博客園對LeTex支持不夠好(不方便,顏色也不好看),所以我把推演的過程放到了 [這個網站] ,下面是推演過程的截圖:
(由於 $c = 2^k$ 的時候,我們可以直接使用位移來實現除法,所以這種情況我們不做討論。)

上圖是原理的推演過程,下面我們來分析一下誤差:

這裡補充說明一下為什麼總誤差 $E$ 滿足的條件是: $E < 1/c$:
例如:當 $a / 10 = q + 0.0$ 的時候,此時當總誤差 $E >= 1.0$ 的時候,q 才會比真實 q 值大1;
更極端的情況:$a / 10 = q + 0.9$ 的時候,此時當總誤差 $E >= 0.1$ 的時候,q 才會比真實 q 值大1。
綜上可得,只要總誤差 $E$ 滿足 $E < 1/c$,即可保證取整後的 q 值等於真實 q 值。
其實,如果向上取整不滿足(1)式,那麼向下取整必然滿足(1)式,為什麼呢?
雖然向上取整的結果是大於真實值的,向下取整的結果是小於真實值的,不管是大於還是小於,我們都稱之為誤差,向下取整的誤差分析跟上面的類似。
我們設向上取整的誤差為 $e$,向下取整的誤差為 $e'$,則必有:$e + e' = 1$,(因為如果向上取整的誤差為0.2,那麼向下取整的誤差必然是0.8)
而如果 $0 <= e < 2^k / c$ 不滿足,意味著必然滿足: $0 <= (1 - e) < 2^k / c$,(這裡 $c$ 是滿足 $2^k < c < 2^(k+1)$ 的,所以 $0.5 < 2^k / c < 1$ )
即有:$0 <= e' < 2^k / c$ ,就是說如果 $e$ 不滿足(1)式,則 $e'$ 必然滿足(1)式。
即使最極端的情況下,$e = 0.5$ 的時候,因為 $0.5 < 2^k / c < 1$,所以 $e = e' = 0.5$ 必然是滿足(1)式的。
知道了原理,那麼我們來實際演算一下 /10 的優化,被除數 c = 10, 優先找一個數 k,滿足 2^k < c < 2^(k+1),那麼 k 為 3,因為 2^3 < 10 < 2^(3+1),我們設要求的相乘的系數為 m, 那麼另 m = [2^(32+k) / c],這裡用向上取整,即 m = [2^(32+3) / 10] = [3435973836.8] = 3435973837,即十六進制表示法的 0xCCCCCCCD,最大誤差為 e = 0.2 (因為我們放大了(3435973837 -3435973836.8) = 0.2),我們看是否滿足(1)式,代入:0 < 0.2 < 2^3 / 10,即 0 < 0.2 < 0.8,成立,所以相乘系數 0xCCCCCCCD 是成立的,且向右位移的位數為 k = 3 位,跟文章前面所演示的一致。
我們再看看編譯器對其他 c 值的優化系數,我們可以得知 /100 的相乘系數為:0x51EB851F, 右移5位,/3 的相乘系數為:0xAAAAAAAB, 右移1位,/5 的相乘系數為:0xCCCCCCCD, 右移2位,其實它就等價於 /10,只是位移少1位,或者說 /10 其實是等價於 /5 的,只是位移量不同而已。/1000 的相乘系數為:0x10624DD3, 右移6位,/125 的相乘系數為:0x10624DD3, 右移3位。
我們發現,其實對於被除數 c ,如果 c 能夠被 $2^N$ 整除,可以先把 $c$ 化為 $c = 2^N * c'$,再對 c' 做上面的優化處理,然後再在右移的位數再加上 N 位右移即可,不過其實不做這一步也是可以的,但是這樣做有利於縮小相乘系數的范圍。
非常類似於32位無符號整型的除法優化,依然以 / 10 為例,優化的結果為:
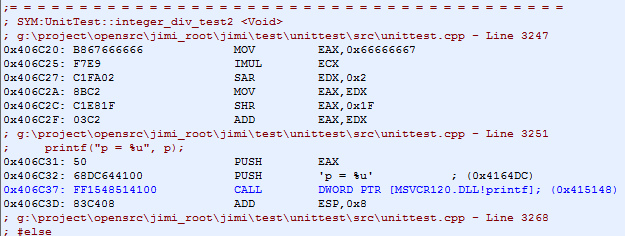
我們可以看到,優化的過程為,乘以一個32位整型 0x66666667,(高位)算術右位移 2 位,再把高位邏輯右移31位(實際是取得高位的符號位),再在原EDX的基礎上再加上這個值(這個值當除數為負數時為1,除數為正數時為0)。當除數 a 為正數時,我們很容易理解,推理也如同上面的32位無符號整型一模一樣,0x66666667 這個數的取值是由32位有符號整型的正數范圍是 0 ~ 2^31-1 決定的,推演過程類似32位無符號整型。
當除數 a 為負數時,情況略微復雜。首先,我們來看看整數取整是怎麼定義的,當 a >= 0 時, | a | 為小於或等於 a 的最小整數,當 a < 0 時, | a | 為大於或等於 a 的最小整數。那麼對於負數,例如:|-0.5| = 大於或等於-0.5的最小整數,即 |-0.5| = 0,依此可得:|-1.5| = -1.0,|-11.3| = -11.0。
我們再以 /10 為例,如果 $a = -5$,則 $a / 10 = -5 / 10 = q + r = (-1.0) + 0.5$,而$|a / 10| = |-5/10| = |-0.5| = 0.0$,如果 $a = -15$,則 $a / 10 = -15 / 10 = q + r = (-2.0) + 0.5$,而 $|-15/10| = |-1.5| = -1.0$,我們看到,為了保證余數 $r$ 的范圍在 $0 <= r < 1.0$,根據前面提到的負整數取整的定義,這裡 $|a/10|$ 取整的值是比 $q$ 的值大 1 的。而 $q$ 的值正好我們在32位無符號整型所得的結果,我們要計算的是 $|a/10|$,所以只需要在 $q$ 值的結果上再加 1 即可。所以有了上面把EDX的符號位右移31位,再跟原EDX值累加的過程,最終累加的結果即為最後所求的 $|a/10|$ 值。
結論:當被除數是常數時,除非你要計算的數值必須強制使用32位有符號整型,否則盡量使用32位無符號整型,因為32位有符號整型的常量除法會比無符號整型多兩條指令,一條位移,一條ADD(加法)指令。
經過上面的推演,我們已經掌握了優化時用來相乘的系數以及位移(右移)的位數,可是為什麼有的編譯器把32位無符號整型的常量除法 /10 也優化成:Value / 10 ~= [ [ (Value * 0x66666667) / 2^32 ] / 2^2 ],這個道理很簡單,只要能夠滿足除數 a 在 0 ~ 2^32-1 范圍內的誤差都不大於 1/c 的話,不管你相乘的數是多少,最終的結果都是成立的。
/ 常數 和 % 常數 是等價的:其實這個優化常用於 itoa() 函數裡,其實大多數情況下,都不會以 /10, /5, /3 的形式出現,多數是跟 % 10, % 5, % 3 一起出現的,如果同時做 /10, % 10 的運算,這兩個運算是可以合並為一次的常數除法優化的,因為 % 10 只不過是 / 10 的求余過程,而得到了 /10,則 % 10 只是一個計算 $r = a - c * q$ 的過程,多一條乘法和一條減法指令而已。而Windows的 itoa() 函數是需要指定 radix(基) 的,10進制必須指定 radix = 10, 因為 radix 是一個變量,因此其內部使用的是 div 指令,這是一個很糟糕的函數。
還有很多的技巧,比如:sprintf()的實現代碼裡,一般都會通過一個變量 base 的改變來實現一個數轉換為8進制,10進制或16進制,即令 base = 8; base = 10; base = 16; 但是編譯器在處理 base = 8, 16 的時候是可以優化為位移的,但很奇怪的是,當 base = 10 的時候使用的卻是 div 指令,這個特點在 Visual Studio 各個版本裡都是如此,包括最新的 VS 2013, 2014,效率是打折扣的。GCC 和 clang 上我未求證,我猜 clang 上有可能能正確優化(當然可能是有前提條件的),有空可以研究一下。但是其實這個問題是可以通過修改代碼來解決的,我們對每個部分的base都用常量來代替就可以了,這樣就不依賴於編譯器優化,因為都指定為常量了,編譯器就明白怎麼做了,沒有歧義。
這裡做個小廣告,推薦一下我的一個項目,我叫它 Jimi,Github地址為:https://github.com/shines77/jimi/ ,目標是實現一個高性能,實用,可伸縮,接口友好,較接近Java, CSharp的C/C++類庫。一開始的靈感來自於OSGi.Net,http://www.iopenworks.com,原意是想實現像OSGi(Open Service Gateway Initiative)那樣可伸縮的可任意搭配的C++類庫,所以原本是想叫Jimu,不過不太好聽,所以改成現在這個名字。由於實現Java那樣的OSGi對於C++目前是不太可行的(由於效率和語言本身的問題),所以方向也變了。裡面包含了上面我提到的一些對 itoa() 和 sprintf() 的優化技巧,雖然還很多東西還不完整,也未做什麼推廣,但是裡面有很多實用的技巧,等待你去發現。
[討論] B計劃之大數乘以10,除以10的快速算法的討論和實現 by liangbch
http://bbs.emath.ac.cn/thread-521-3-1.html
[CSDN論壇]利用移位指令來實現一個數除以10
http://bbs.csdn.net/topics/320096074