“在我介紹別的算法之前,你先來講一講你是准備如何使用線段樹來解決這個問題的吧?”小Hi雖然做好了講解的准備,但是還是希望能夠一步步引導小Ho進行思考,於是這般說道。
“唔……那我先從線段樹的定義說起吧:線段樹其實本質就是用一棵樹來維護一段區間上和某個子區間相關的值——例如區間和、區間最大最小值一類的。”小Ho說道:“它的具體做法是這樣的,這棵樹的根節點表示了整段區間,根節點的左兒子節點表示了這段區間的前半部分,根節點的右兒子節點表示了這段區間的後半部分——並以此類推,對於這棵樹的每個節點,如果這個節點所表示的區間的長度大於1,則令其左兒子節點表示這段區間的前半部分,令其右兒子表示這段區間的後半部分。以一段長度為10的區間為例,我所建立出的線段樹應該是這樣子的。”
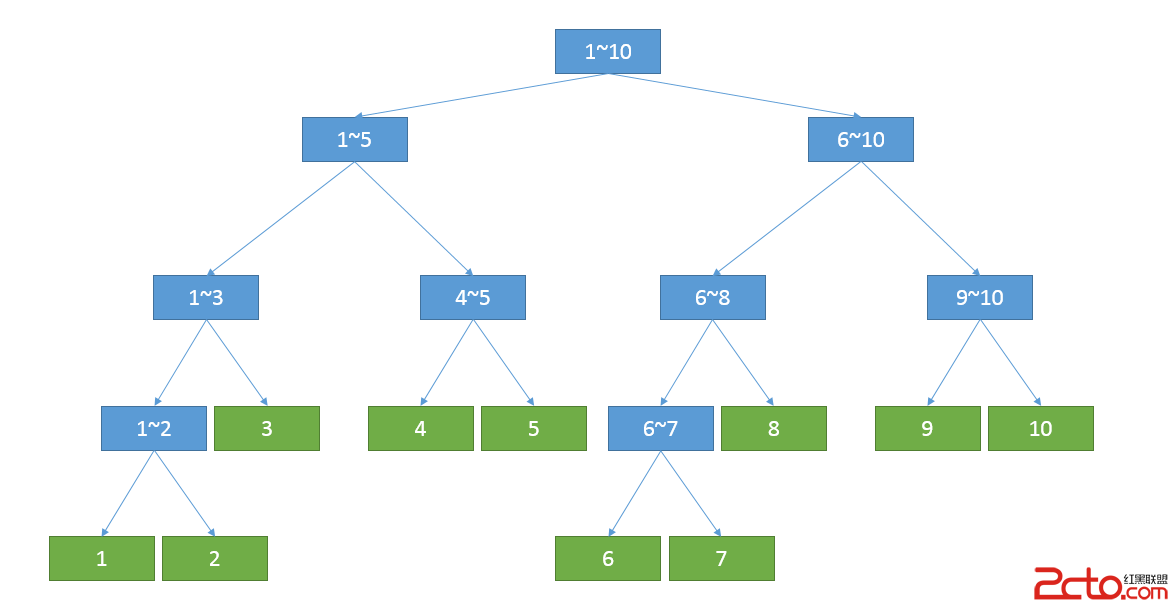
“畫的還湊合,但是這樣一棵樹有什麼用呢?”小Hi明知故問道。
“就以RMQ問題為例吧——RMQ問題要求的是求解一段區間中的最小值,那麼我不妨效仿ST算法,先對一些可能會用到的區間求解這個最小值!而既然我要是用線段樹來解決這個問題的,那麼我不妨就將每一個節點對應的區間中的最小值都求解出來。”小Ho道。
“那我給你這樣一組數據,你將這個預處理的結果給我計算一下?”小Hi又出難題。

“好啊!你這數據正好也只有10個位置,那麼我便直接用這棵樹了。”只見小Ho刷刷兩筆便在之前繪下的二叉樹上寫下了每個節點對應的區間中的最小值:“事實上這樣一步相當好計算,由於每個非葉子節點所對應的區間都正好由它的兩個兒子節點所對應的區間拼湊而成——那麼只需要像ST那樣,這樣一個節點所對應的區間中的最小值便是它的兩個兒子節點所對應的區間中的最小值中更小的那一個。這樣我只需要O(N)的時間復雜度就可以計算出這棵樹來。”
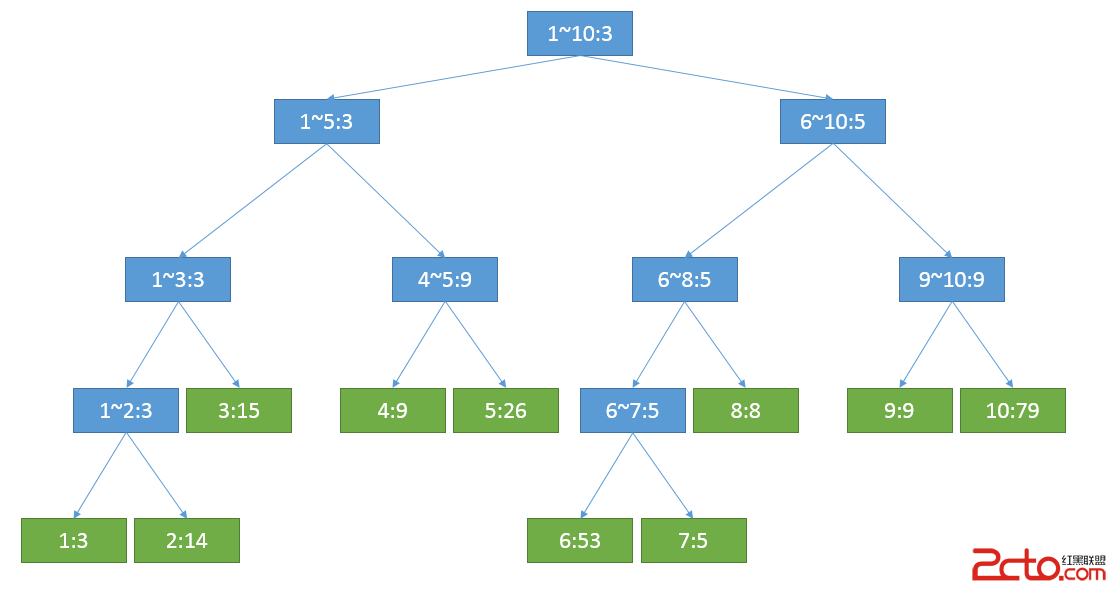
小Hi點了點頭,繼續問道:“我算是明白了,但是你這樣一棵樹統計出來的區間比ST算法統計出來的區間要少了很多,你還能夠使用很快的算法進行查詢麼?更何況還有修改呢?”
小Ho笑了笑:“我先從簡單的說起吧——修改,當某個位置的商品的重量發生改變的時候,對應的,就是這棵樹的某個葉子節點的值發生了變化——但是和ST算法不同,包含這個節點的區間,便只有這個節點的所有祖先節點,而這樣的節點數量事實上是很少的——只有O(log(N))級別。也就是說,當一次修改操作發生的時候,我只需要改變數量在O(log(N))級別的節點的值就可以完成操作了,修改的時間復雜度是O(log(N))。”
小Hi道:“是這樣沒錯~算你過關!但是呢,還是像我之前所說的,你是准備如何使用數量在O(N)級別的區間來應付所有的詢問呢?”
小Ho的笑容仍未退去:“這個其實也很簡單!我要做的事情其實就是——將一個詢問的區間拆成若干個我已經計算出來的區間(在ST算法中是拆成了2個的區間),這樣對於這些區間已經計算出的最小值求最小值的話,我就可以知道詢問的整個區間中的最小值是多少了!”
“那你准備如何分解詢問的區間呢?”小Hi問道。
小Ho思索了一會,道:“這個問題其實很簡單!我從線段樹的根開始,對於當前訪問的線段樹節點t, 設其對應的區間為[A, B], 如果詢問的區間[l, r]完全處於前半段或者後半段——即r <= (A + B)/2或者l > (A + B) / 2,那麼遞歸進入t對應的子節點進行處理(因為另一棵子樹中顯然不會有任何區間需要用到)。否則的話,則把詢問區間分成2部分[l, (A + B) / 2]和[(A + B) / 2 + 1, r],並且分別進入t的左右子樹處理這兩段詢問區間(因為2棵子樹中顯然都有區間需要用到)!當然了,如果[A, B]正好覆蓋了[l, r]的話,就可以直接返回之前計算的t這棵子樹中的最小值了。還是之前那個例子,如果我要詢問[3, 9]這段區間,我的最終結果會是這樣的——橙色部分標注的區間。”
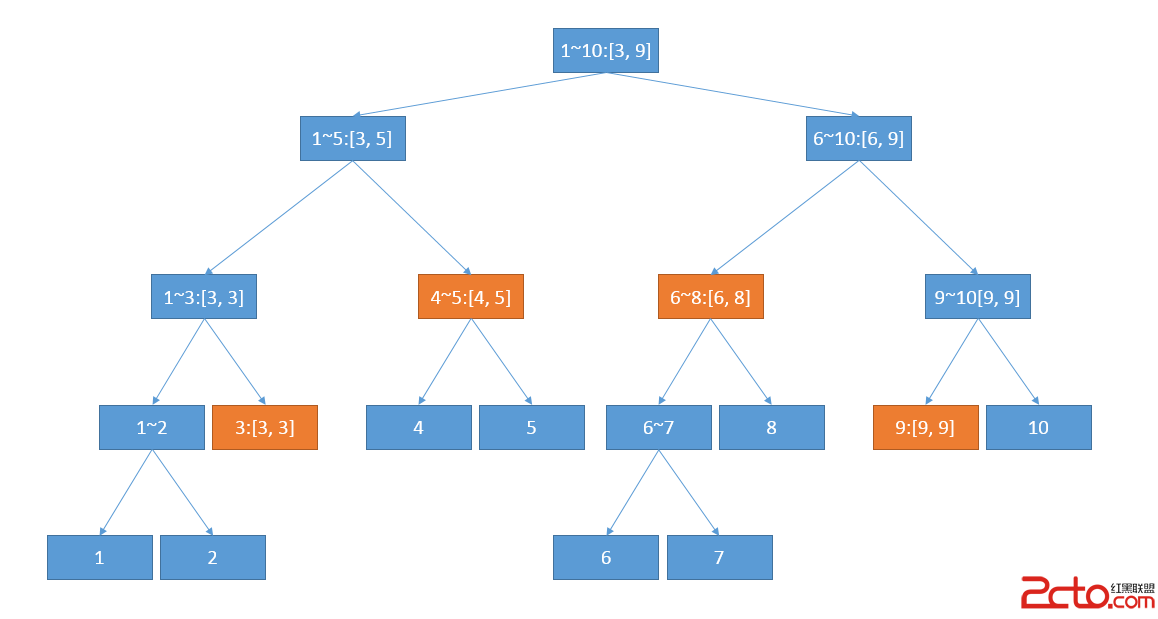
“首先[3, 9]分解成了[3, 5]和[6, 9]兩個區間,而[3, 5]分解成了[3, 3]和[4, 5]——均沒有必要繼續分解,[6, 9]分解成了[6, 8]和[9, 9]——同樣也沒有必要繼續分解了。每一步的分解都是必要的,所以這已經是最好的分解方法了。”
小Hi滿意的點了點頭,道:“聽起來還不錯?但是你這樣分解的話,區間的個數你能保證麼?萬一很多怎麼辦?”
小Ho思索了一會,接著道:“不會的,除了第一次分解成2個區間的操作可能會將區間個數翻倍外,之後每一次分解的時候所處理的區間都肯定有一條邊是和當前節點對應的重合的(即l=A或者r=B),也就是說即使再進行分解,分解出的兩個區間中也一定會有一個區間是不需要再進行分解的,也就是區間的總數是在深度這個級別的,所以也是O(logN)的。”
“看來你還挺清楚的,那麼要不你再總結一下,我就算你過關,然後我們就可以開始講解後面的問題了~”
小Ho道:“好的!首先我會根據初始數據,使用O(N)的時間構建一棵最原始的線段樹,這個過程中我會使用子節點的值來計算父親節點的值,從而避免冗余計算。然後對於每一次操作,如果是一次修改的話,我就將修改的節點和這個節點的所有祖先節點的值都進行更新,可以用O(logN)的時間復雜度完成。而如果是一次詢問的話,我會使用上面描述的方法來對詢問區間進行分解,這樣雖然不像ST算法那樣是O(1),但是卻實現了上一次所提到的‘平衡’,無論是修改還是查詢的時間復雜度都是O(logN)的,所以我這個算法最終的時間復雜度會是O(N + Q * log(N)),在這個數據規模下是綽綽有余的!”
“嗯~ o(* ̄▽ ̄*)o 不錯喲~那麼就到這裡吧!”小Hi笑容滿滿道:“趕緊去吃早飯吧!”
對hdu 1166 經典題目敵兵布陣 (單點更新) 加了詳細的解釋
題意為給定n個數的序列,編號1到n,提供三種操作 add p x 把第p個數增加x, sub p x 把第p個數減去x, query l r, 查詢從l到r個數的和(即區間[l,r]的和).
#include#include #include #include using namespace std; const int maxn=50010; struct SegTree { int l,r; int sum; }segTree[maxn<<2]; void Build(int i,int l,int r) { segTree[i].l=l; segTree[i].r=r; int mid=(l+r)>>1; if(segTree[i].l==segTree[i].r) { scanf(%d,&segTree[i].sum); return;//千萬別忘了這一句!!! } Build(i<<1,l,mid); Build((i<<1)|1,mid+1,r); segTree[i].sum=segTree[i<<1].sum+segTree[(i<<1)|1].sum; } void Add(int i,int p,int add) { segTree[i].sum+=add; int l=segTree[i].l; int r=segTree[i].r; if(l==r) return; int mid=(l+r)>>1; //為什麼這麼寫呢?修改某個點,只要修改該點以及包含該點的祖先節點就好了; //我們是從根節點開始相加的。那麼最重要的任務就是判斷根節點的左右孩子哪個包含所要修改的那個點,該點只存在於一個孩子中,因為 //根節點的兩個孩子所代表的區間是不相交的。所以我們要麼去左孩子節點增加值,要麼去右孩子節點增加值,怎麼判斷呢;對於根節點區間[L,R]; //令mid=(L+R)/2; 其左孩子代表的區間為[L,mid],右孩子區間代表的是[mid+1,R],這樣就很明顯了,如果要修改的位置<=mid時,那我們肯定是要去左 //孩子的,因為只有左孩子的區間才包括該點啊,相反如果>mid時,就只能去右孩子了。這裡就是關鍵,所以增加的操作就是從根節點開始向下,不斷拐彎 //不斷增加值,直到找到葉子節點為止。 if(p<=mid) Add(i<<1,p,add); else Add((i<<1)|1,p,add); } int Sum(int i,int l,int r) { //為什麼這麼寫呢?該功能是查詢區間[l,r]的和,我們稱其為目標區間; //我們是從根節點開始查詢的。 //首先考慮的是到底是查詢根節點本身,還是它的左孩子,還是它的右孩子呢,如果l,r正好是根節點所代表的區間,那麼直接返回根節點的sum值就可以了 //如果不是的話,就要考慮到左右孩子去了,設根節點區間[L,R],令mid=(L+R)/2,則左孩子區間為[L,mid],右孩子區間為[mid+1,R],怎樣根據孩子區間去找目標區間呢 //如果目標區間的r<=mid時,那麼該目標區間一定存在左孩子中,如果目標區間的l>mid時,那麼目標區間一定存在右孩子中,如果mid在l,r之間時,那麼我們就要 //查詢左右兩個孩子。 //注意,如果所建的樹中當查詢到某一個節點時,其節點代表的區間正好是該函數的參數時,那麼查到該節點就直接返回其sum值即可,無需向下查詢到葉子節點 // 如果沒有的話,那麼就得查詢到葉子節點,把葉子節點的sum值相加 // if(segTree[i].l==segTree[i].r)//這一句寫的大錯特錯!!!定要注意 // return segTree[i].sum; if(segTree[i].l==l&&segTree[i].r==r) return segTree[i].sum; int ans=0; int mid=((segTree[i].l+segTree[i].r)>>1); if(r<=mid) ans=Sum(i<<1,l,r); else if(l>mid) ans=Sum((i<<1)|1,l,r); else ans=Sum(i<<1,l,mid)+Sum((i<<1)|1,mid+1,r); return ans; } int main() { char cm[10]; int n; int t;scanf(%d,&t); int p,add,l,r; for(int cas=1;cas<=t;++cas) { printf(Case %d: ,cas); scanf(%d,&n); Build(1,1,n); while(scanf(%s,cm)) { if(cm[0]=='E') break; if(cm[0]=='A') { scanf(%d%d,&p,&add); Add(1,p,add); } else if(cm[0]=='S') { scanf(%d%d,&p,&add); Add(1,p,-add); } else { scanf(%d%d,&l,&r); printf(%d ,Sum(1,l,r)); } } } return 0; }