本文由單源最短路徑路徑問題開始,而後描述Bellman-Ford算法,到具體闡述Dijkstra算法,闡述詳細剖析Dijkstra算法的每一個步驟,教你徹底理解此Dijkstra算法。
一、單源最短路徑問題
我們知道,單源最短路徑問題:已知圖G=(V,E),要求找出從某個定源頂點s<-V,到每個v<-V的最短路徑。簡單來說,就是一個圖G中,找到一個定點s,然後以s為起點,要求找出s到圖G中其余各個點的最短距離或路徑。
此單源最短路徑問題有以下幾個變形:
I、 單終點最短路徑問題: 每個頂點v到指定終點t的最短路徑問題。即單源最短路徑問題的相對問題。
II、 單對頂點最短路徑問題:給定頂點u和v,找出從u到v的一條最短路徑。
III、每對頂點間最短路徑問題:
針對任意每倆個頂點u和v,找出從u到v的最短路徑。最簡單的想法是,將每個頂點作為源點,運行一次單源算法即可以解決這個問題。當然,還有更好的辦法。
二、Bellman-Ford 算法
1、回路問題
一條最短路徑不能包含負權回路,也不能包含正權回路。一些最短路徑的算法,如Dijkstra 算法,要求圖中所有的邊的權值都是非負的,如在公路地圖上,找一條從定點s到目的頂點v的最短路徑問題。
2、Bellman-Ford 算法
而Bellman-Ford 算法,則允許輸入圖中存在負權邊,只要不存在從源點可達的負權回路,即可。簡單的說,圖中可以存在負權邊,但此條負權邊,構不成負權回路,不影響回路的形成。且,Bellman-Ford 算法本身,便是可判斷圖中是否存在從源點可達的負權回路,若存在負權回路,算法返回FALSE,若不存在,返回TRUE。
Bellman-Ford 算法的具體描述
BELLMAN-FORD(G, w, s)
- INITIALIZE-SINGLE-SOURCE(G, s) //對每個頂點初始化 ,O(V)
- for i ← 1 to |V[G]| - 1
- do for each edge (u, v) ∈ E[G]
- do RELAX(u, v, w) //針對每個頂點(V-1個),都運用松弛技術O(E),計為O(v-1)*E))
- for each edge (u, v) ∈ E[G]
- do if d[v] > d[u] + w(u, v)
- then return FALSE //檢測圖中每條邊,判斷是否包含負權回路,
- //若d[v]>d[u]+w(u,v),則表示包含,返回FALSE,
- return TRUE //不包含負權回路,返回TRUE
Bellman-Ford 算法的時間復雜度,由上可得為OV*E)。
3、關於判斷圖中是否包含負權回路的問題:
根據定理,我們假定,u是v的父輩,或父母,那麼,當G(V,E)是一個有向圖或無向圖(且不包含任何負權回路),s<-V,s為G的任意一個頂點,則對任意邊(u,v)<-V,有
d[s,v] <= d[s,u]+1
此定理的詳細證明,可參考算法導論一書上,第22章中引理22.1的證明。或者根據第24章中通過三角不等式論證Bellman-Ford算法的正確性,也可得出上述定理的變形。
即假設圖G中不包含負權回路,可證得
- d[v]=$(s,u)
- <=$(s,u)+w(u,v) //根據三角不等式
- =d[u]+w[u,v]
所以,在不包含負權回路的圖中,是可以得出d[v]<=d[u]+w(u,v)。
於是,就不難理解,在上述Bellman-Ford 算法中, if d[v] > d[u]+w(u,v),=> 包含負權回路,返回FASLE
else if =>不包含負權回路,返回TRUE。
ok,咱們,接下來,立馬切入Dijkstra 算法。
三、深入淺出,徹底解剖Dijkstra 算法
I、松弛技術RELAX的介紹
Dijkstra 算法使用了松弛技術,對每個頂點v<-V,都設置一個屬性d[v],用來描述從源點s到v的最短路徑上權值的上界,
稱為最短路徑的估計。
首先,得用OV)的時間,來對最短路徑的估計,和對前驅進行初始化工作。
- INITIALIZE-SINGLE-SOURCE(G, s)
- for each vertex v ∈ V[G]
- do d[v] ← ∞
- π[v] ← NIL //OV)
- d[s] 0
- RELAX(u, v, w)
- if d[v] > d[u] + w(u, v)
- then d[v] ← d[u] + w(u, v)
- π[v] ← u //OE)圖。
II、Dijkstra 算法
此Dijkstra 算法分三個步驟,INSERT (第3行), EXTRACT-MIN (第5行), 和DECREASE-KEY(第8行的RELAX,調用此減小關鍵字的操作)。
- DIJKSTRA(G, w, s)
- INITIALIZE-SINGLE-SOURCE(G, s) //對每個頂點初始化 ,O(V)
- S ← Ø
- Q ← V[G] //INSERT,O(1)
- while Q ≠ Ø
- do u ← EXTRACT-MIN(Q) //簡單的O(V*V);二叉/項堆,和FIB-HEAP的話,則都為O(V*lgV)。
- S ← S ∪{u}
- for each vertex v ∈ Adj[u]
- do RELAX(u, v, w) //簡單方式:O(E),二叉/項堆,E*O(lgV),FIB-HEAP,E*O(1)。
四、Dijkstra 算法的運行時間
在繼續闡述之前,得先聲明一個問題,DIJKSTRAG,w,s)算法中的第5行,EXTRACT-MIN(Q),最小優先隊列的具體實現。而Dijkstra 算法的運行時間,則與此最小優先隊列的采取何種具體實現,有關。
最小優先隊列三種實現方法:
1、利用從1至|V| 編好號的頂點,簡單地將每一個d[v]存入一個數組中對應的第v項,如上述DIJKSTRAG,w,s)所示,Dijkstra 算法的運行時間為O(V^2+E)。
2、如果是二叉/項堆實現最小優先隊列的話,EXTRACT-MIN(Q)的運行時間為O(V*lgV),所以,Dijkstra 算法的運行時間為O(V*lgV+E*lgV),若所有頂點都是從源點可達的話,O(V+E)*lgV)=OE*lgV)。當是稀疏圖時,則E=O(V^2/lgV),此Dijkstra 算法的運行時間為O(V^2)。
3、采用斐波那契堆實現最小優先隊列的話,EXTRACT-MIN(Q)的運行時間為O(V*lgV),所以,此Dijkstra 算法的運行時間即為O(V*lgV+E)。
綜上所述,此最小優先隊列的三種實現方法比較如下:

當|V|<<|E|時,采用DIJKSTRAG,w,s)+ FIB-HEAP-EXTRACT-MIN(Q),即斐波那契堆實現最小優先隊列的話,
優勢就體現出來了。
五、Dijkstra 算法 + FIB-HEAP-EXTRACT-MIN(H),斐波那契堆實現最小優先隊列
由以上內容,我們已經知道,用斐波那契堆來實現最小優先隊列,可以將運行時間提升到OVlgV+E)。|V|個EXTRACT-MIN 操作,每個平攤代價為OlgV),|E|個DECREASE-KEY操作的每個平攤時間為O1)。
下面,重點闡述DIJKSTRA(G, w, s)中,斐波那契堆實現最小優先隊列的操作。
由上,我們已經知道,DIJKSTRA算法包含以下的三個步驟:
INSERT (第3行), EXTRACT-MIN (第5行), 和DECREASE-KEY(第8行的RELAX)。
先直接給出Dijkstra 算法 + FIB-HEAP-EXTRACT-MIN(H)的算法:
- DIJKSTRA(G, w, s)
- INITIALIZE-SINGLE-SOURCE(G, s)
- S ← Ø
- Q ← V[G] //第3行,INSERT操作,O1)
- while Q ≠ Ø
- do u ← EXTRACT-MIN(Q) //第5行,EXTRACT-MIN操作,V*lgV
- S ← S ∪{u}
- for each vertex v ∈ Adj[u]
- do RELAX(u, v, w) //第8行,RELAX操作,E*O(1)
- FIB-HEAP-EXTRACT-MIN(H) //平攤代價為OlgV)
- z ← min[H]
- if z ≠ NIL
- then for each child x of z
- do add x to the root list of H
- p[x] ← NIL
- remove z from the root list of H
- if z = right[z]
- then min[H] ← NIL
- else min[H] ← right[z]
- CONSOLIDATE(H)
- n[H] ← n[H] - 1
- return z
六、Dijkstra 算法 +fibonacci堆各項步驟的具體分析
ok,接下來,具體分步驟闡述以上各個操作:
第3行的INSERT操作:
- FIB-HEAP-INSERT(H, x) //平攤代價,O1).
- degree[x] ← 0
- p[x] ← NIL
- child[x] ← NIL
- left[x] ← x
- right[x] ← x
- mark[x] ← FALSE
- concatenate the root list containing x with root list H
- if min[H] = NIL or key[x] < key[min[H]]
- then min[H] ← x
- n[H] ← n[H] + 1
第5行的EXTRACT-MIN操作:
- FIB-HEAP-EXTRACT-MIN(H) //平攤代價為OlgV)
- z ← min[H]
- if z ≠ NIL
- then for each child x of z
- do add x to the root list of H
- p[x] ← NIL
- remove z from the root list of H
- if z = right[z]
- then min[H] ← NIL
- else min[H] ← right[z]
- CONSOLIDATE(H) //CONSOLIDATE算法在下面,給出。
- n[H] ← n[H] - 1
- return z
下圖是FIB-HEAP-EXTRACT-MIN 的過程示意圖:
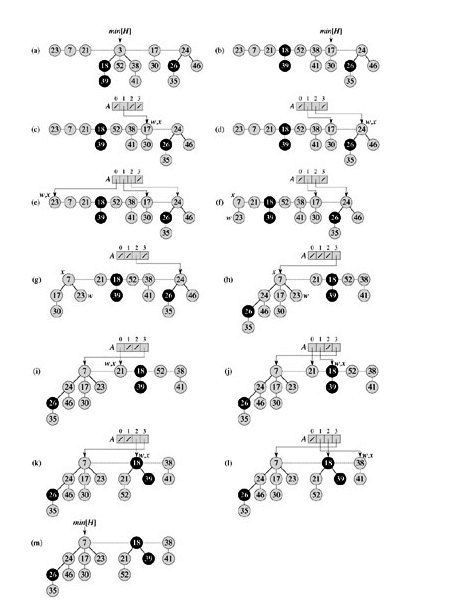
- CONSOLIDATE(H)
- for i ← 0 to D(n[H])
- do A[i] ← NIL
- for each node w in the root list of H
- do x ← w
- d ← degree[x] //子女數
- while A[d] ≠ NIL
- do y ← A[d]
- if key[x] > key[y]
- then exchange x <-> y
- FIB-HEAP-LINK(H, y, x) //下面給出。
- A[d] ← NIL
- d ← d + 1
- A[d] ← x
- min[H] ← NIL
- for i ← 0 to D(n[H])
- do if A[i] ≠ NIL
- then add A[i] to the root list of H
- if min[H] = NIL or key[A[i]] < key[min[H]]
- then min[H] ← A[i]
- FIB-HEAP-LINK(H, y, x) //y鏈接至 x。
- remove y from the root list of H
- make y a child of x, incrementing degree[x]
- mark[y] ← FALSE
第8行的RELAX的操作,已上已經給出:
- RELAX(u, v, w)
- if d[v] > d[u] + w(u, v)
- then d[v] ← d[u] + w(u, v)
- π[v] ← u //OE)
一般來說,在Dijkstra 算法中,DECREASE-KEY的調用次數遠多於EXTRACT-MIN的調用,
所以在不增加EXTRACT-MIN 操作的平攤時間前提下,盡量減小DECREASE-KEY操作的平攤時間,都能獲得對比二叉堆更快的實現。
以下,是二叉堆,二項堆,斐波那契堆的各項操作的時間復雜度的比較:
操作 二叉堆(最壞) 二項堆(最壞) 斐波那契堆(平攤)
MAKE-HEAP Θ(1) Θ(1) Θ(1)
INSERT Θ(lg n) O(lg n) Θ(1)
MINIMUM Θ(1) O(lg n) Θ(1)
EXTRACT-MIN Θ(lg n) Θ(lg n) O(lg n)
UNION Θ(n) O(lg n) Θ(1)
DECREASE-KEY Θ(lg n) Θ(lg n) Θ(1)
DELETE Θ(lg n) Θ(lg n) O(lg n)
斐波那契堆,日後會在本BLOG內,更進一步的深入與具體闡述。且同時,此文,會不斷的加深與擴展。