匈牙利算法是由匈牙利數學家Edmonds提出的,用增廣路徑求二分圖最大匹配的算法。
聽起來高端,其實說白了就是:
假設不存在單相思(單身狗偷偷抹眼淚),在一個同性戀不合法的國家裡(不存在任何歧視#正色),有一些男人和女人,他們互相之間存在一些互相愛戀的關系。而匈牙利算法就是要促成盡量多的男女配對。
如下圖:
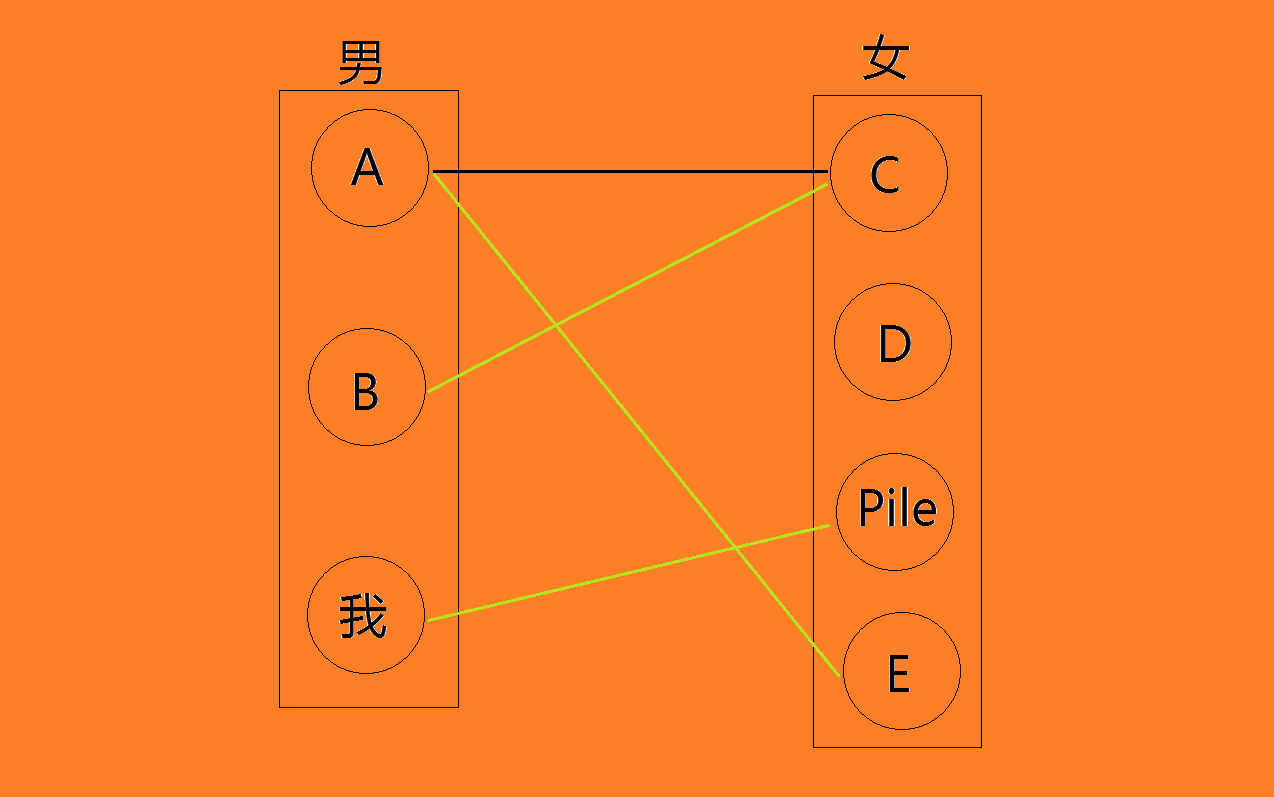
綠色標注的就是這張圖的一個最大二分圖匹配。
先提一個下面會提到的名詞:
增廣路:若P是圖G中一條連通兩個未匹配頂點的路徑,並且屬於M的邊和不屬於M的邊(即已匹配和待匹配的邊)在P上交替出現,則稱P為相對於M的一條增廣路徑。
下面講講匈牙利算法的思路:
1、依次從一個部分的每個頂點出發,尋找一條增廣路;
2、遍歷所有以當前點為起點的邊,若找到一條增廣路,就更新匹配數,並返回1;否則重復二,直至所有邊被遍歷;
3、若以當前點為起點的所有邊被遍歷仍未找到一條可增廣路,返回1。
顯然,由於尋找增廣路的過程需要深搜,所以匈牙利算法是一個基於dfs的算法。思路很簡單,所以我就不貼偽代碼了才不是因為懶而且還不會寫偽代碼(劃掉),反正hero是裸題,題解裡也有模板。
題目描述:
現在電視台有一種節目叫做超級英雄,大概的流程就是每位選手到台上回答主持人的幾個問題,然後根據回答問題的多少獲得不同數目的獎品或獎金。主持人問題准備了若干道題目,只有當選手正確回答一道題後,才能進入下一題,否則就被淘汰。為了增加節目的趣味性並適當降低難度,主持人總提供給選手幾個“錦囊妙計”,比如求助現場觀眾,或者去掉若干個錯誤答案(選擇題)等等。 這裡,我們把規則稍微改變一下。假設主持人總共有m道題,選手有n種不同的“錦囊妙計”。主持人規定,每道題都可以從兩種“錦囊妙計”中選擇一種,而每種“錦囊妙計”只能用一次。我們又假設一道題使用了它允許的錦囊妙計後,就一定能正確回答,順利進入下一題。現在我來到了節目現場,可是我實在是太笨了,以至於一道題也不會做,每道題只好借助使用“錦囊妙計”來通過。如果我事先就知道了每道題能夠使用哪兩種“錦囊妙計”,那麼你能告訴我怎樣選擇才能通過最多的題數嗎?
輸入:
輸入文件的一行是兩個正整數n和m(0 < n <1001,0 < m < 1001)表示總共有n中“錦囊妙計”,編號為0~n-1,總共有m個問題。
以下的m行,每行兩個數,分別表示第m個問題可以使用的“錦囊妙計”的編號。
注意,每種編號的“錦囊妙計”只能使用一次,同一個問題的兩個“錦囊妙計”可能一樣。
輸出:
第一行為最多能通過的題數p。
樣例輸入:
5 6
3 2
2 0
0 3
0 4
3 2
3 2
樣例輸出:
4
數據范圍:
0 < n , m < 1001
絕對的裸題,裸得讓我懷疑這是我在bzoj上見到的。附上鏈接→_→http://www.lydsy.com/JudgeOnline/problem.php?id=1191
代碼如下:
