通過考察各種二叉鏈表,不管兒叉樹的形態如何,空鏈域的個數總是多過非空鏈域的個數。准確的說,n各結點的二叉鏈表共有2n個鏈域,非空鏈域為n-1個,但其中的空鏈域卻有n+1個。如下圖所示。
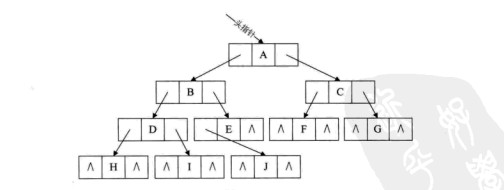
因此,提出了一種方法,利用原來的空鏈域存放指針,指向樹中其他結點。這種指針稱為線索。
記ptr指向二叉鏈表中的一個結點,以下是建立線索的規則:
(1)如果ptr->lchild為空,則存放指向中序遍歷序列中該結點的前驅結點。這個結點稱為ptr的中序前驅;
(2)如果ptr->rchild為空,則存放指向中序遍歷序列中該結點的後繼結點。這個結點稱為ptr的中序後繼;
顯然,在決定lchild是指向左孩子還是 前驅,rchild是指向右孩子還是後繼,需要一個區分標志的。因此,我們在每個結點再增設兩個標志域ltag和rtag,注意ltag和rtag只是區 分0或1數字的布爾型變量,其占用內存空間要小於像lchild和rchild的指針變量。結點結構如下所示。
![]()
其中:
(1)ltag為0時指向該結點的左孩子,為1時指向該結點的前驅;
(2)rtag為0時指向該結點的右孩子,為1時指向該結點的後繼;
(3)因此對於上圖的二叉鏈表圖可以修改為下圖的養子。
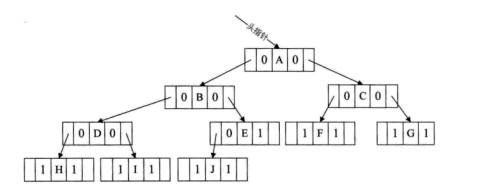
1.樹節點采用class定義,class bintree{};
class bintree
{
public:
char data;
bintree *leftchild,*rightchild;//存儲左右節點
int lefttag,righttag;//標記左右節點是指針還是線索,1表示是線索,0表示是指針
};
2.首先創建一顆二叉樹
輸入包括一行,為由空格分隔開的各節點,按照二叉樹的分層遍歷順序給出,每個節點形式如X(Y,num),X表示該節點,Y表示父節點,num為0,1,2中的一個,0 表示根節點,1表示為父節點的左子節點,2表示為父節點的右子節點。輸出為一行,為中序遍歷的結果.
輸入:A(0,0) B(A,1) C(A,2) D(B,1) E(B,2) F(C,1) G(D,1) H(D,2)
輸出:G D H B E A F C
創建二叉樹的代碼可以根據自己的習慣自己編寫函數。以下為個人習慣:
bintree *createtree(){
bintree *root = new bintree;
bintree *parent;
string in_string;
while(cin>>in_string){
if(in_string[2]-'0'==0){
root->data = in_string[0];
root->leftchild = root->rightchild = NULL;
root->lefttag = root->righttag=0;
continue;
}
parent = find(root,in_string[2]);
if(in_string[4]-'0'==1){
bintree *newnode = new bintree;
newnode->data = in_string[0];
newnode->leftchild = newnode->rightchild = NULL;
newnode->lefttag = newnode->righttag=0;
parent->leftchild = newnode;
}else if(in_string[4]-'0'==2){
bintree *newnode = new bintree;
newnode->data = in_string[0];
newnode->leftchild = newnode->rightchild = NULL;
newnode->lefttag = newnode->righttag = 0;
parent->rightchild = newnode;
}
if(getchar()=='\n')
break;
}
return root;
}
3.寫出中序線索化過程的函數,在添加頭結點線索化函數中調用
因為要線索化當前節點的後繼不方便,所以用pre記錄節點t的前一個節點,可以確定t為pre的後繼,那麼,每次都是確定當前節點的前驅和該節點上一個節點pre的後繼(參照代碼)。
bintree *pre;//用來記錄上一個節點,即當前節點的前驅,當前節點為pre的後繼
bintree *inthreading(bintree *root){ bintree *t = root; if(t){ inthreading(t->leftchild);//線索化左子樹
/****!!!!!****/ if(t->leftchild==NULL){//左子樹為空,則將其線索化,使其指向它的前驅 t->lefttag = 1; t->leftchild = pre; }
//因為要線索化當前節點的後繼不方便,所以用pre記錄節點t的前一個節點,可以確定t為pre的後繼,那麼,每次都是確定當前節點的前驅和該節點上一個節點pre的後繼 if(pre->rightchild==NULL){//前一個節點右子樹為空,則將其線索化,使其指向它的後繼 pre->righttag = 1; pre->rightchild = t; } pre = t;
/****!!!!!*****/ inthreading(t->rightchild);//線索化右子樹 } return root; }
4.通過添加頭結點的方式將其線索化
上述/***!!!!!****/ /****!!!!!****/中間部分代碼做了這樣的事情:
if(!p->leftchild)表示如果某結點的左指針域為空,因為其前驅結點剛剛訪問過,賦值了pre,所以可以將pre賦值給p->leftchild,並修改p->lefttag = 1(也就是定義為1)以完成前驅結點的線索化。
後繼就麻煩一些。因為此時p結點的後繼還沒 有訪問到,因此只能對它的前驅結點pre的右指針rightchild做判斷,if(!pre->rightchild)表示如果為空,則p就是pre的後繼,於是 pre->rightchild = p,並且設置pre->righttag =1,完成後繼結點的線索化。
完成前驅和後繼的判斷後,不要忘記當前結點p賦值給pre,以便於下一次使用。
有了線索二叉樹後,對它進行遍歷時,其實就等於操作一個雙向鏈表結構。
和雙向鏈表結點一樣,在二叉樹鏈表上添加一 個頭結點,如下圖所示,並令其leftchild域的指針指向二叉樹的根結點(圖中第一步),其rightchild域的指針指向中序遍歷訪問時的最後一個結點(圖中第 二步)。反之,令二叉樹的中序序列中第一個結點中,leftchild域指針和最後一個結點的rightchild域指針均指向頭結點(圖中第三和第四步)。這樣的好處 是:我們既可以從第一個結點起順後繼進行遍歷,也可以從最後一個結點起順前驅進行遍歷。
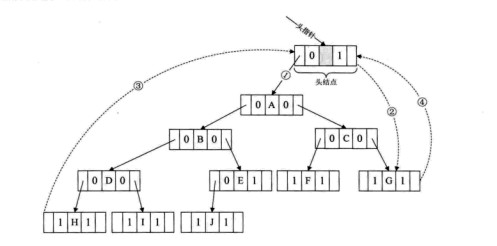
bintree *addheadthread(bintree *root,bintree *head){
bintree *t = root;
head->righttag=0;
head->rightchild = head;
if(t==NULL){
head->lefttag = 0;
head->leftchild = head;
}else{
pre = head;
head->lefttag = 0;
head->leftchild = t;//完成圖中所示的步驟1
inthreading(t);//在該過程中就已經完成了線索化和圖中所示的步驟3
pre->rightchild = head;//完成步驟4
pre->righttag = 1;
head->rightchild = pre;//完成步驟2
}
}
5.中序遍歷線索化二叉樹
void inorder(bintree *head){
bintree *t = head->leftchild;//通過頭結點進入根節點
while(t!=head){//表示已遍歷完成,指針t已經回到了頭結點
while(t->lefttag==0)//循環找到中序遍歷的第一個節點
t = t->leftchild;
cout<<t->data<<" ";
while(t->righttag==1&&t->rightchild!=head){//不斷的輸出後繼,直到某個節點rightchild所指的不是後繼,即righttag!=1
t = t->rightchild;
cout<<t->data<<" ";
}
t = t->rightchild;//進入右子樹
}
}
6.完整代碼
/***********線索二叉樹************
Author:ChengSong
Language:C++
Time:2015/12/23
********************************/
#include<iostream>
#include<cstdlib>
#include<string>
#include<cstdio>
#include<stack>
#define type char
using namespace std;
class bintree
{
public:
char data;
bintree *leftchild,*rightchild;
int lefttag,righttag;
};
bintree *pre;
bintree *find(bintree *root,char in_data){
bintree *t = root;
bintree *node;
if(t==NULL)return NULL;
if(t->data == in_data)return t;
else{
node = find(t->leftchild,in_data);
if(node) return node;
else return find(t->rightchild,in_data);
}
}
bintree *createtree(){
bintree *root = new bintree;
bintree *parent;
string in_string;
while(cin>>in_string){
if(in_string[2]-'0'==0){
root->data = in_string[0];
root->leftchild = root->rightchild = NULL;
root->lefttag = root->righttag=0;
continue;
}
parent = find(root,in_string[2]);
if(in_string[4]-'0'==1){
bintree *newnode = new bintree;
newnode->data = in_string[0];
newnode->leftchild = newnode->rightchild = NULL;
newnode->lefttag = newnode->righttag=0;
parent->leftchild = newnode;
}else if(in_string[4]-'0'==2){
bintree *newnode = new bintree;
newnode->data = in_string[0];
newnode->leftchild = newnode->rightchild = NULL;
newnode->lefttag = newnode->righttag = 0;
parent->rightchild = newnode;
}
if(getchar()=='\n')
break;
}
return root;
}
bintree *inthreading(bintree *root){
bintree *t = root;
if(t){
inthreading(t->leftchild);
if(t->leftchild==NULL){
t->lefttag = 1;
t->leftchild = pre;
}
if(pre->rightchild==NULL){
pre->righttag = 1;
pre->rightchild = t;
}
pre = t;
inthreading(t->rightchild);
}
return root;
}
bintree *addheadthread(bintree *root,bintree *head){
bintree *t = root;
head->righttag=0;
head->rightchild = head;
if(t==NULL){
head->lefttag = 0;
head->leftchild = head;
}else{
pre = head;
head->lefttag = 0;
head->leftchild = t;
inthreading(t);
pre->rightchild = head;
pre->righttag = 1;
head->rightchild = pre;
}
}
void inorder(bintree *head){
bintree *t = head->leftchild;
while(t!=head){
while(t->lefttag==0)
t = t->leftchild;
cout<<t->data<<" ";
while(t->righttag==1&&t->rightchild!=head){
t = t->rightchild;
cout<<t->data<<" ";
}
t = t->rightchild;
}
}
int main(){
bintree *root = createtree();
bintree *head = new bintree;
addheadthread(root,head);
inorder(head);
return 0;
}
7.樣例輸入與輸出
輸入:
A(0,0) B(A,1) C(A,2) D(B,1) E(B,2) F(C,1) G(D,1) H(D,2)
輸出:
G D H B E A F C