本文地址:http://www.cnblogs.com/archimedes/p/matrix-multiply.html,轉載請注明源地址。
原理:矩陣相乘最重要的方法是一般矩陣乘積。它只有在第一個矩陣的欄數(column)和第二個矩陣的列數(row)相同時才有定義。一般單指矩陣乘積時,指的便是一般矩陣乘積。若A為m×n矩陣,B為n×p矩陣,則他們的乘積AB會是一個m×p矩陣。其乘積矩陣的元素如下面式子得出:
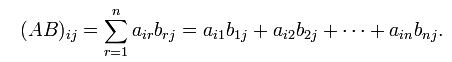
代碼如下:
struct mat{
int n, m;
double data[MAXN][MAXN];
};
int mul(mat& c, const mat& a, const mat& b){
int i, j, k;
if (a.m != b.n)
return 0;
c.n = a.n;
c.m = b.m;
for (i = 0; i < c.n; i++)
for (j = 0; j < c.m; j++)
for (c.data[i][j] = k = 0; k < a.m; k++)
c.data[i][j] += a.data[i][k] * b.data[k][j];
return 1;
}
時間復雜度:O(n3)
C = AB
將A, B, C分成相等大小的方塊矩陣:
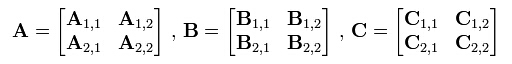
C11=A11B11+A12B21 (2)
C12=A11B12+A12B22 (3)
C21=A21B11+A22B21 (4)
C22=A21B12+A22B22 (5)
如果n=2,則2個2階方陣的乘積可以直接用(2)-(5)式計算出來,共需8次乘法和4次加法。當子矩陣的階大於2時,為求2個子矩陣的積,可以繼續將子矩陣分塊,直到子矩陣的階降為2。這樣,就產生了一個分治降階的遞歸算法。依此算法,計算2個n階方陣的乘積轉化為計算8個n/2階方陣的乘積和4個n/2階方陣的加法。2個n/2×n/2矩陣的加法顯然可以在c*n2/4時間內完成,這裡c是一個常數。因此,上述分治法的計算時間耗費T(n)應該滿足:
T(2) = b
T(n) = 8T(n / 2) + cn2 (n > 2)
由上式可知:分治法的運用,方陣的乘法的算法效率並沒有提高!
分治法的設計思想:將一個難以直接解決的大問題,分割成一些規模較小的相同問題,以便各個擊破,分而治之。
任何一個可以用計算機求解的問題所需的計算時間都與其規模有關。問題的規模越小,越容易直接求解,解題所需的計算時間也越少。例如,對於n個元素的排。n=2時,只要作一次比較即可排好序。n=3時序問題,當n=1時,不需任何計算只要作3次比較即可,…。而當n較大時,問題就不那麼容易處理了。要想直接解決一個規模較大的問題,有時是相當困難的。
分治法所能解決的問題一般具有以下幾個特征:
1.可縮性。問題的規模縮小到一定的程度就可以容易地解決;
2.最有子結構性。問題可以分解為若干個規模較小的相同問題;
3.可合性。利用該問題分解出的子問題的解可以合並為該問題的解;
4.獨立性。該問題所分解出的各個子問題是相互獨立的,即子問 題之間不包含公共的子子問題。
分治思想與遞歸就像一對孿生兄弟,經常同時應用在算法設計中,並由此產生高效的算法!
傳統方法2個2階方陣相乘需要8次乘法。按照上述分治法的思想可以看出,要想減少乘法運算次數,關鍵在於計算2個2階方陣的乘積時,能否用少於8次的乘法運算。Strassen提出了一種新的算法來計算2個2階方陣的乘積。他的算法只用了7次乘法運算,但增加了加、減法的運算次數。這7次乘法是:
M1=A11(B12-B22)
M2=(A11+A12)B22
M3=(A21+A22)B11
M4=A22(B21-B11)
M5=(A11+A22)(B11+B22)
M6=(A12-A22)(B21+B22)
M7=(A11-A21)(B11+B12)
做了7次乘法後,再做若干次加、減法:
C11=M5+M4-M2+M6
C12=M1+M2
C21=M3+M4
C22=M5+M1-M3-M7
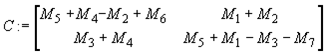
算法效率分析:
Strassen矩陣乘積分治算法中,用了7次對於n/2階矩陣乘積的遞歸調用和18次n/2階矩陣的加減運算。由此可知,該算法的所需的計算時間T(n)滿足如下的遞歸方程:
T(2) = b
T(n) = 7T(n / 2) + cn2 (n > 2)
按照解遞歸方程的套用公式法,其解為T(n)=O(nlog7)≈O(n2.81)。由此可見,Strassen矩陣乘法的計算時間復雜性比普通矩陣乘法有階的改進。
數據的存儲結構:
二維數組(弊端:必須宏定義一常量N)
二重指針 (擺脫宏定義的限制,但程序變得繁瑣)
原始矩陣:
A,B,C(C=AB)
分塊矩陣:
A11,A12,A21,A22(對方陣A分成四塊)
B11,B12,B21,B22(對方陣B分成四塊)
七塊關鍵陣:
M1,M2,M3,M4,M5,M6,M7
中間方陣:
AA,BB(計算加法時作一個橋梁)
二級指針定義說明:
int **c;
c = (int**)malloc(n * sizeof(int));
for(int i = 0; i < n; i++)
c[i] = (int *)malloc(n * sizeof(int));
兩矩陣相加問題:
//矩陣加法:
void add(int n, int A[][N], int B[][N], int R[][N])
{
int i, j;
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
R[i][j] = A[i][j] + B[i][j];
}
兩矩陣相減問題:
//矩陣減法:
void sub(int n,int A[][N],int B[][N],int R[][N])
{
int i,j;
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
R[i][j] = A[i][j] - B[i][j];
}
兩方陣相乘問題:
//階為2的方陣相乘:
void multiply(int A[][N],int B[][N],int R[][N])
{
int M1 = A[0][1] * (B[0][1] - B[1][1]);
int M2 = (A[0][0] + A[0][1]) * B[1][1];
int M3 = (A[1][0] + A[1][1]) * B[0][0];
int M4 = A[1][1] * (B[1][0] - B[0][0]);
int M5 = (A[0][0] + A[1][1]) * (B[0][0] + B[1][1]);
int M6 = (A[0][1] - A[1][1]) * (B[1][0] + B[1][1]);
int M7 = (A[0][0] - A[1][0]) * (B[0][0] + B[0][1]);
R[0][0] = M5 + M4 - M2 + M6;
R[0][1] = M1 + M2;
R[1][0] = M3 + M4;
R[1][1] = M5 + M1 - M3 - M7;
}
將大的方陣劃分的問題
//分塊函數
void divide(int A[][N], int n, int X11[][N], int X12[][N], int X21[][N], int X22[][N] )
{
int i, j;
for(i = 0; i < (n / 2); i++)
for(j = 0; j < (n / 2); j++) {
X11[i][j] = A[i][j];
X12[i][j] = A[i][j + (n / 2)];
X21[i][j] = A[i + (n / 2)][j];
X22[i][j] = A[i + (n / 2)][j + (n / 2)];
}
}
完整代碼如下:
#include<stdio.h>
#include<math.h>
#define N 4
//二階矩陣相乘
void Matrix_Multiply(int A[][N], int B[][N], int C[][N]) {
for(int i = 0; i < 2; i++) {
for(int j = 0; j < 2; j++) {
C[i][j] = 0;
for(int t = 0; t < 2; t++) {
C[i][j] = C[i][j] + A[i][t] * B[t][j];
}
}
}
}
//矩陣加法:
void add(int n, int A[][N], int B[][N], int R[][N])
{
int i, j;
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
R[i][j] = A[i][j] + B[i][j];
}
//矩陣減法:
void sub(int n, int A[][N], int B[][N], int R[][N])
{
int i,j;
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
R[i][j] = A[i][j] - B[i][j];
}
void strassen(int n, int A[][N], int B[][N], int C[][N])
{
int i, j;
int A11[N][N], A12[N][N], A21[N][N], A22[N][N];
int B11[N][N], B12[N][N], B21[N][N], B22[N][N];
int C11[N][N], C12[N][N], C21[N][N], C22[N][N];
int AA[N][N], BB[N][N];
int M1[N][N], M2[N][N], M3[N][N], M4[N][N], M5[N][N], M6[N][N], M7[N][N];
if(n == 2) {
Matrix_Multiply(A, B, C);
} else {
for(i = 0; i < n / 2; i++) {
for(j = 0; j < n / 2; j++) {
A11[i][j] = A[i][j];
A12[i][j] = A[i][j + n / 2];
A21[i][j] = A[i + n / 2][j];
A22[i][j] = A[i + n / 2][j + n / 2];
B11[i][j] = B[i][j];
B12[i][j] = B[i][j + n / 2];
B21[i][j] = B[i + n /2][j];
B22[i][j] = B[i + n /2][j + n / 2];
}
}
sub(n / 2, B12, B22, BB);
strassen(n / 2, A11, BB, M1);
add(n / 2, A11, A12, AA);
strassen(n / 2, AA, B22, M2);
add(n / 2, A21, A22, AA);
strassen(n / 2, AA, B11, M3);
sub(n / 2, B21, B11, BB);
strassen(n / 2, A22, BB, M4);
add(n / 2, A11, A22, AA);
add(n / 2, B11, B22, BB);
strassen(n / 2, AA, BB, M5);
sub(n / 2, A12, A22, AA);
add(n / 2, B21, B22, BB);
strassen(n / 2, AA, BB, M6);
sub(n / 2, A11, A21, AA);
add(n / 2, B11, B12, BB);
strassen(n / 2, AA, BB, M7);
//C11 = M5 + M4 - M2 + M6
add(n / 2, M5, M4, AA);
sub(n / 2, M6, M2, BB);
add(n / 2, AA, BB, C11);
//C12 = M1 + M2
add(n / 2, M1, M2, C12);
//C21 = M3 + M4
add(n / 2, M3, M4, C21);
//C22 = M5 + M1 - M3 - M7
sub(n / 2, M5, M3, AA);
sub(n / 2, M1, M7, BB);
add(n / 2, AA, BB, C22);
for(i = 0; i < n / 2; i++) {
for(j = 0; j < n / 2; j++) {
C[i][j] = C11[i][j];
C[i][j + n / 2] = C12[i][j];
C[i + n / 2][j] = C21[i][j];
C[i + n / 2][j + n / 2] = C22[i][j];
}
}
}
}
int main(void)
{
int A[N][N], B[N][N], C[N][N];
printf("input A: \n");
for(int i = 0; i < N; i++)
for(int j = 0; j < N; j++)
scanf("%d", &A[i][j]);
printf("input B: \n");
for(int i = 0; i < N; i++)
for(int j = 0; j < N; j++)
scanf("%d", &B[i][j]);
strassen(N, A, B, C);
printf("C:\n");
for(int i = 0; i < N; i++)
for(int j = 0; j < N; j++) {
printf("%d ", C[i][j]);
if(j > 0 && j % 3 == 0)
printf("\n");
}
return 0;
}
2行2列矩陣 乘以 2行3列矩陣 所得的矩陣是:2行3列矩陣
最後結果為:|1 3 5|
|0 4 6|
|a b| |e f g| |ae+bh af+bi ag+bk|
|c d| 乘以 |h i k| 等於 |ce+dh cf+di cg+dk|
不知道你能不能看出來,
前一矩陣的第一行對應元乘以後一矩陣第一列對應元之和為新矩陣的第一行第一列的元素。
例如:1*0+1*1=1
前一矩陣的第一行對應元乘以後一矩陣第二列對應元之和為新矩陣的第一行第二列的元素。
例如:1*2+1*1=3
前一矩陣的第一行對應元乘以後一矩陣第三列對應元之和為新矩陣的第一行第三列的元素。
例如:1*3+1*2=5
前一矩陣的第二行對應元乘以後一矩陣第一列對應元之和為新矩陣的第二行第一列的元素。
例如:2*0+0*1=0
前一矩陣的第二行對應元乘以後一矩陣第二列對應元之和為新矩陣的第二行第二列的元素。
例如:2*2+0*1=4
前一矩陣的第二行對應元乘以後一矩陣第三列對應元之和為新矩陣的第二行第三列的元素。
例如:2*3+0*2=6
int A[N][N];
int B[N][N];
int C[N][N];
for(int* pA = a, *pB = B, *pC = C; pA != B + N*N; ++pA, ++pB, ++pC)
{
*pC = *pA * *pB;
}
復雜度O(3N^2)