簡介
圖表示點之間的關系,在C#中通過節點對象的集合來表示點(Vertex),用鄰接矩陣(adjacency matrix)來表示點之間的關系。下面來看C#實現。
PS:本片文章是我復習的筆記,代碼注釋很全。勿吐槽。
表示點的對象
下面實現代碼:
class Vertex
{
publicstring Data;
publicbool IsVisited;
public Vertex(string Vertexdata)
{
Data = Vertexdata;
}
}
每個節點包含兩個字段,分別為節點數據以及表示是否被訪問過的一個布爾類型。
表示圖的對象
圖中除了需要點的集合和鄰接矩陣之外,還需要一些基本的向圖中添加或刪除元素的方法,以及一個構造方法來對圖進行初始化。
publicclass Graph
{
//圖中所能包含的點上限privateconstint Number = 10;
//頂點數組private Vertex[] vertiexes;
//鄰接矩陣publicint[,] adjmatrix;
//統計當前圖中有幾個點int numVerts = 0;
//初始化圖public Graph()
{
//初始化鄰接矩陣和頂點數組
adjmatrix = new Int32[Number, Number];
vertiexes = new Vertex[Number];
//將代表鄰接矩陣的表全初始化為0for (int i = 0; i < Number; i++)
{
for (int j = 0; j < Number; j++)
{
adjmatrix[i, j] = 0;
}
}
}
//向圖中添加節點publicvoid AddVertex(String v)
{
vertiexes[numVerts] = new Vertex(v);
numVerts++;
}
//向圖中添加有向邊publicvoid AddEdge(int vertex1, int vertex2)
{
adjmatrix[vertex1, vertex2] = 1;
//adjmatrix[vertex2, vertex1] = 1;
}
//顯示點publicvoid DisplayVert(int vertexPosition)
{
Console.WriteLine(vertiexes[vertexPosition]+"");
}
}
拓撲排序(TopSort)
拓撲排序是對一個有向的,並且不是環路的圖中所有的頂點線性化。需要如下幾個步驟
1.首先找到沒有後繼的節點。
2.將這個節點加入線性棧中
3.在圖中刪除這個節點
4.重復步驟1,2,3
因此,首先需要找到後繼節點的方法:
//尋找圖中沒有後繼節點的點
//具體表現為鄰接矩陣中某一列全為0//此時返回行號,如果找不到返回-1privateint FindNoSuccessor()
{
bool isEdge;
//循環行for (int i = 0; i < numVerts; i++)
{
isEdge = false;
//循環列,有一個1就跳出循環for (int j = 0; j < numVerts; j++)
{
if (adjmatrix[i, j] == 1)
{
isEdge = true;
break;
}
}
if (!isEdge)
{
return i;
}
}
return -1;
}
此外還需要刪除圖中點的方法,這個方法不僅需要刪除圖中對應位置的點,還需要刪除鄰接矩陣對應的行和列,因此設置了兩個輔助方法,見代碼。
//刪除圖中的點//需要兩個操作,分別從數組中刪除點//從鄰接矩陣中消去被刪點的行和列privatevoid DelVertex(int vert)
{
//保證不越界if (vert <= numVerts - 1)
{
//刪除節點for (int i = vert; i < numVerts; i++)
{
vertiexes[i] = vertiexes[i + 1];
}
//刪除鄰接矩陣的行for (int j = vert; j < numVerts; j++)
{
MoveRow(j, numVerts);
}
//刪除鄰接矩陣中的列,因為已經刪了行,所以少一列for (int k = vert; k < numVerts - 1;k++ )
{
MoveCol(k, numVerts-1);
}
//刪除後減少一個
numVerts--;
}
}
//輔助方法,移動鄰接矩陣中的行privatevoid MoveRow(int row, int length)
{
for (int col = row; col < numVerts; col++)
{
adjmatrix[row, col] = adjmatrix[row + 1, col];
}
}
//輔助方法,移動鄰接矩陣中的列privatevoid MoveCol(int col, int length)
{
for (int row = col; row < numVerts; row++)
{
adjmatrix[row, col] = adjmatrix[row, col+1];
}
}
有了這幾個方法,就可以按照步驟開始拓撲排序了:
//拓撲排序//找到沒有後繼節點的節點,刪除,加入一個棧,然後輸出publicvoid TopSort()
{
int origVerts = numVerts;
//存放返回節點的棧
System.Collections.Stack result = new Stack();
while (numVerts > 0)
{
//找到第一個沒有後繼節點的節點int currVertex = FindNoSuccessor();
if (currVertex == -1)
{
Console.WriteLine("圖為環路圖,不能搞拓撲排序");
return;
}
//如果找到,將其加入返回結果棧
result.Push(vertiexes[currVertex].Data);
//然後刪除此節點
DelVertex(currVertex);
}
/*輸出排序後的結果*/
Console.Write("拓撲排序的順序為:");
while (result.Count > 0)
{
Console.Write(result.Pop()+"");
}
/*輸出排序後的結果*/
}
下面,對拓撲排序進行測試,代碼如下:
staticvoid Main(string[] args)
{
Graph g = new Graph();
g.AddVertex("A");
g.AddVertex("B");
g.AddVertex("C");
g.AddVertex("D");
g.AddEdge(0, 1);
g.AddEdge(1, 2);
g.AddEdge(2, 3);
g.AddEdge(3, 4);
g.TopSort();
Console.ReadKey();
}
測試結果:
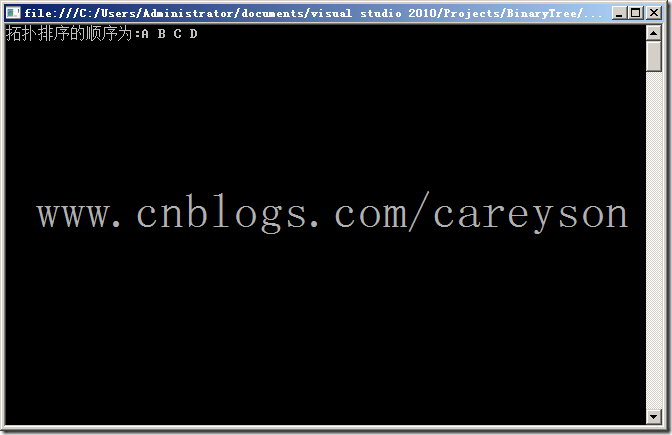
圖的遍歷
很多時候,我們需要知道從圖中給定點到另一個點是否能走通,比如幾個車站之間是否可以連接。這時我們需要對圖進行查找,查找大概可以分為兩類,深度優先遍歷和廣度優先遍歷,下面先來看深度優先遍歷。
深度優先遍歷(Depth-First Search)
深度優先遍歷首先從一個點開始,到一條路徑結束,然後循環找第二條路徑,到結束,依此往復。
首先我們需要一個輔助方法返回給定的點最近一個連接並且未被訪問過的序號。
//從鄰接矩陣查找給定點第一個相鄰且未被訪問過的點//參數v是給定點在鄰接矩陣的行privateint GetAdjUnvisitedVertex(int v)
{
for (int j = 0; j < numVerts; j++)
{
if (adjmatrix[v,j]==1 && vertiexes[j].IsVisited == false)
{
return j;
}
}
return -1;
}
下面,就可以進行深度優先遍歷了:
//深度優先遍歷publicvoid DepthFirstSearch()
{
//聲明一個存儲臨時結果的棧
System.Collections.Stack s = new Stack();
//先訪問第一個節點
vertiexes[0].IsVisited = true;
DisplayVert(0);
s.Push(0);
int v;
while (s.Count > 0)
{
//獲得和當前節點連接的未訪問過節點的序號
v = GetAdjUnvisitedVertex((int)s.Peek());
if (v == -1)
{
s.Pop();
}
else
{
//標記為已經被訪問過
vertiexes[v].IsVisited = true;
DisplayVert(v);
s.Push(v);
}
}
//重置所有節點為未訪問過for (int u = 0; u < numVerts; u++)
{
vertiexes[u].IsVisited = false;
}
}
廣度優先遍歷(Breadth-First Search)
廣度優先遍歷首先遍歷層級。算法如下:
//廣度優先遍歷publicvoid BreadthFirstSearch()
{
System.Collections.Queue q = new Queue();
/*首先訪問第一個節點*/
vertiexes[0].IsVisited = true;
DisplayVert(0);
q.Enqueue(0);
/*第一個節點訪問結束*/int vert1, vert2;
while (q.Count > 0)
{
/*首先訪問同層級第一個節點*/
vert1 = (int)q.Dequeue();
vert2 = GetAdjUnvisitedVertex(vert1);
/*結束*/while (vert2 != -1)
{
/*首先訪問第二個節點*/
vertiexes[vert2].IsVisited = true;
DisplayVert(vert2);
q.Enqueue(vert2);
//尋找鄰接的
vert2 = GetAdjUnvisitedVertex(vert1);
}
}
//重置所有節點為未訪問過for (int u = 0; u < numVerts; u++)
{
vertiexes[u].IsVisited = false;
}
}
下面我們來測試深度優先和廣度優先遍歷:
我們的測試生成一個如下的圖:
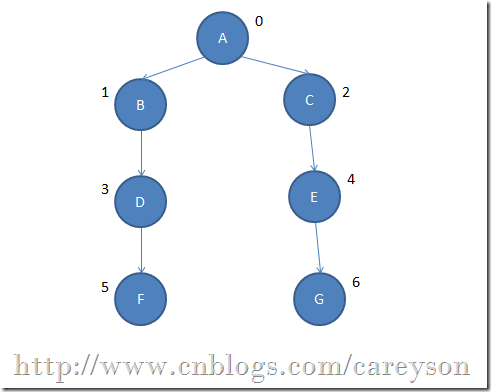
測試代碼:
staticvoid Main(string[] args)
{
Graph g = new Graph();
g.AddVertex("A");
g.AddVertex("B");
g.AddVertex("C");
g.AddVertex("D");
g.AddVertex("E");
g.AddVertex("F");
g.AddVertex("G");
g.AddEdge(0, 1);
g.AddEdge(0, 2);
g.AddEdge(1, 3);
g.AddEdge(2, 4);
g.AddEdge(3, 5);
g.AddEdge(4, 6);
Console.WriteLine("\n深度優先遍歷");
g.DepthFirstSearch();
Console.WriteLine("\n廣度優先遍歷");
g.BreadthFirstSearch();
Console.ReadKey();
}