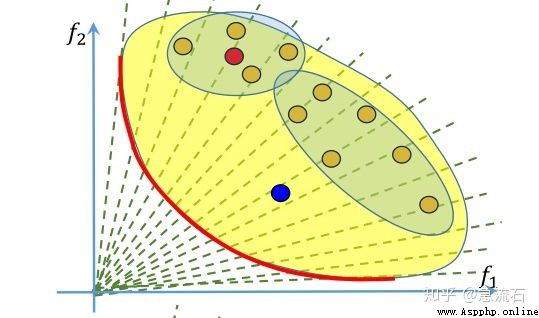
答:每個解對應的是一組權重,即子問題,紅點附近的四個點,也就是它的鄰居怎麼確定呢?由權重來確定,算法初始化階段就確定了每個權重對應的鄰居,也就是每個子問題的鄰居子問題。權重的鄰居通過歐式距離來判斷。取最近的幾個。
https://www.cnblogs.com/Twobox/p/16408751.html
https://www.zhihu.com/question/263555181?sort=created
其中兩個回答都挺好的
1. 輸入N m # N表示取點密度 m表示問題維度 1.1 輸入 T # 表示取最近的T個作為鄰居 2. 生成均勻分布權重向量 2.1 計算每個權重向量之間的歐拉距離 3. 權重向量個數即為:初始種群個數 4. 初始化種群,每個個體一一對應權重 4.1 更具權重之間距離,取前T個作為鄰居person 5. EP = 空 # 維護成最優前沿 6. 計算最初的全局最優Z # 把每個帶入f1 f2中,取最小值 z1 z2 7. 開始循環N代 7.1對於每個個體,在領域中選取2個個體進行交叉變異,獲得2個新個體 7.1.1更新全局解z 7.2在領域中隨機選擇2個個體,用新個與舊個體進行對比 # 新個體帶入子目標問題,直接對比值即可 7.3如果更優,則替換舊個體dna 7.4更新EP # 如果有別接收的新解,將新解與EP每一個進行比較,刪除被新解支配的,如果新解沒有被舊解支配,那麼加入EP
代碼實現設計
# 分析 需要維護的數據結構: 某個體最近的T位鄰居: 可以考慮采用對象列表即可 均勻分布的權重向量:一個二維ndarray數組即可 權重向量與個體對應關系:個體對象,直接保存權重向量數組 權重向量之間的距離矩陣:開局初始化,不變的 EP list,裡面的個體是對象的引用 z list 目標函數集合,F list domain list # 接口設計 class Person attribute: dns:一維ndarray weight_vector: 一維ndarray neighbor: list<Person> o_func:Objective_Function 目標函數 function: mutation cross_get_two_new_dna:返回2段新dna compare#與子代比較 accept_new_dna choice_two_person:p1,p2 class Moead_Util attribute: N M T: o_func:Objective_Function pm:變異概率 EP:[dna1,dna2,..] weight_vectors:二維數組 Euler_distance:二維數組 pip_size Z:[] # 這裡面元素為一維ndarray數組,即dna,即解 function: init_mean_vector:二維數組 init_Euler_distance:二維數組 init_population:[] init_Z:一維屬豬 update_ep update_Z class Objective_Function: attribute: F:[] domain:[[0,1],[],[]] function: get_one_function:Objective_Function
1 import numpy as np 2 3 4 class Person: 5 def __init__(self, dna): 6 self.dna = dna 7 self.weight_vector = None 8 self.neighbor = None 9 self.o_func = None # 目標函數 10 11 self.dns_len = len(dna) 12 13 def set_info(self, weight_vector, neighbor, o_func): 14 self.weight_vector = weight_vector 15 self.neighbor = neighbor 16 self.o_func = o_func# 目標函數 17 18 def mutation_dna(self, one_dna): 19 i = np.random.randint(0, self.dns_len) 20 low = self.o_func.domain[i][0] 21 high = self.o_func.domain[i][1] 22 new_v = np.random.rand() * (high - low) + low 23 one_dna[i] = new_v 24 return one_dna 25 26 def mutation(self): 27 i = np.random.randint(0, self.dns_len) 28 low = self.o_func.domain[i][0] 29 high = self.o_func.domain[i][1] 30 new_v = np.random.rand() * (high - low) + low 31 self.dna[i] = new_v 32 33 @staticmethod 34 def cross_get_two_new_dna(p1, p2): 35 # 單點交叉 36 cut_i = np.random.randint(1, p1.dns_len - 1) 37 dna1 = p1.dna.copy() 38 dna2 = p2.dna.copy() 39 temp = dna1[cut_i:].copy() 40 dna1[cut_i:] = dna2[cut_i:] 41 dna2[cut_i:] = temp 42 return dna1, dna2 43 44 def compare(self, son_dna): 45 F = self.o_func.f_funcs 46 f_x_son_dna = [] 47 f_x_self = [] 48 for f in F: 49 f_x_son_dna.append(f(son_dna)) 50 f_x_self.append(f(self.dna)) 51 fit_son_dna = np.array(f_x_son_dna) * self.weight_vector 52 fit_self = np.array(f_x_self) * self.weight_vector 53 return fit_son_dna.sum() - fit_self.sum() 54 55 def accept_new_dna(self, new_dna): 56 self.dna = new_dna 57 58 def choice_two_person(self): 59 neighbor = self.neighbor 60 neighbor_len = len(neighbor) 61 idx = np.random.randint(0, neighbor_len, size=2) 62 p1 = self.neighbor[idx[0]] 63 p2 = self.neighbor[idx[1]] 64 return p1, p2
1 from collections import defaultdict
2
3 import numpy as np
4
5
6 def zdt4_f1(x_list):
7 return x_list[0]
8
9
10 def zdt4_gx(x_list):
11 sum = 1 + 10 * (10 - 1)
12 for i in range(1, 10):
13 sum += x_list[i] ** 2 - 10 * np.cos(4 * np.pi * x_list[i])
14 return sum
15
16
17 def zdt4_f2(x_list):
18 gx_ans = zdt4_gx(x_list)
19 if x_list[0] < 0:
20 print("????: x_list[0] < 0:", x_list[0])
21 if gx_ans < 0:
22 print("gx_ans < 0", gx_ans)
23 if (x_list[0] / gx_ans) <= 0:
24 print("x_list[0] / gx_ans<0:", x_list[0] / gx_ans)
25
26 ans = 1 - np.sqrt(x_list[0] / gx_ans)
27 return ans
28
29 def zdt3_f1(x):
30 return x[0]
31
32
33 def zdt3_gx(x):
34 if x[:].sum() < 0:
35 print(x[1:].sum(), x[1:])
36 ans = 1 + 9 / 29 * x[1:].sum()
37 return ans
38
39
40 def zdt3_f2(x):
41 g = zdt3_gx(x)
42 ans = 1 - np.sqrt(x[0] / g) - (x[0] / g) * np.sin(10 * np.pi * x[0])
43 return ans
44
45
46 class Objective_Function:
47 function_dic = defaultdict(lambda: None)
48
49 def __init__(self, f_funcs, domain):
50 self.f_funcs = f_funcs
51 self.domain = domain
52
53 @staticmethod
54 def get_one_function(name):
55 if Objective_Function.function_dic[name] is not None:
56 return Objective_Function.function_dic[name]
57
58 if name == "zdt4":
59 f_funcs = [zdt4_f1, zdt4_f2]
60 domain = [[0, 1]]
61 for i in range(9):
62 domain.append([-5, 5])
63 Objective_Function.function_dic[name] = Objective_Function(f_funcs, domain)
64 return Objective_Function.function_dic[name]
65
66 if name == "zdt3":
67 f_funcs = [zdt3_f1, zdt3_f2]
68 domain = [[0, 1] for i in range(30)]
69 Objective_Function.function_dic[name] = Objective_Function(f_funcs, domain)
70 return Objective_Function.function_dic[name] 1 import numpy as np
2
3 from GA.MOEAD.Person import Person
4
5
6 def distribution_number(sum, m):
7 # 取m個數,數的和為N
8 if m == 1:
9 return [[sum]]
10 vectors = []
11 for i in range(1, sum - (m - 1) + 1):
12 right_vec = distribution_number(sum - i, m - 1)
13 a = [i]
14 for item in right_vec:
15 vectors.append(a + item)
16 return vectors
17
18
19 class Moead_Util:
20 def __init__(self, N, m, T, o_func, pm):
21 self.N = N
22 self.m = m
23 self.T = T # 鄰居大小限制
24 self.o_func = o_func
25 self.pm = pm # 變異概率
26
27 self.Z = np.zeros(shape=m)
28
29 self.EP = [] # 前沿
30 self.EP_fx = [] # ep對應的目標值
31 self.weight_vectors = None # 均勻權重向量
32 self.Euler_distance = None # 歐拉距離矩陣
33 self.pip_size = -1
34
35 self.pop = None
36 # self.pop_dna = None
37
38 def init_mean_vector(self):
39 vectors = distribution_number(self.N + self.m, self.m)
40 vectors = (np.array(vectors) - 1) / self.N
41 self.weight_vectors = vectors
42 self.pip_size = len(vectors)
43 return vectors
44
45 def init_Euler_distance(self):
46 vectors = self.weight_vectors
47 v_len = len(vectors)
48
49 Euler_distance = np.zeros((v_len, v_len))
50 for i in range(v_len):
51 for j in range(v_len):
52 distance = ((vectors[i] - vectors[j]) ** 2).sum()
53 Euler_distance[i][j] = distance
54
55 self.Euler_distance = Euler_distance
56 return Euler_distance
57
58 def init_population(self):
59 pop_size = self.pip_size
60 dna_len = len(self.o_func.domain)
61 pop = []
62 pop_dna = np.random.random(size=(pop_size, dna_len))
63 # 初始個體的 dna
64 for i in range(pop_size):
65 pop.append(Person(pop_dna[i]))
66
67 # 初始個體的 weight_vector, neighbor, o_func
68 for i in range(pop_size):
69 # weight_vector, neighbor, o_func
70 person = pop[i]
71 distance = self.Euler_distance[i]
72 sort_arg = np.argsort(distance)
73 weight_vector = self.weight_vectors[i]
74 # neighbor = pop[sort_arg][:self.T]
75 neighbor = []
76 for i in range(self.T):
77 neighbor.append(pop[sort_arg[i]])
78
79 o_func = self.o_func
80 person.set_info(weight_vector, neighbor, o_func)
81 self.pop = pop
82 # self.pop_dna = pop_dna
83
84 return pop
85
86 def init_Z(self):
87 Z = np.full(shape=self.m, fill_value=float("inf"))
88 for person in self.pop:
89 for i in range(len(self.o_func.f_funcs)):
90 f = self.o_func.f_funcs[i]
91 # f_x_i:某個體,在第i目標上的值
92 f_x_i = f(person.dna)
93 if f_x_i < Z[i]:
94 Z[i] = f_x_i
95
96 self.Z = Z
97
98 def get_fx(self, dna):
99 fx = []
100 for f in self.o_func.f_funcs:
101 fx.append(f(dna))
102 return fx
103
104 def update_ep(self, new_dna):
105 # 將新解與EP每一個進行比較,刪除被新解支配的
106 # 如果新解沒有被舊解支配,則保留
107 new_dna_fx = self.get_fx(new_dna)
108 accept_new = True # 是否將新解加入EP
109 # print(f"准備開始循環: EP長度{len(self.EP)}")
110 for i in range(len(self.EP) - 1, -1, -1): # 從後往前遍歷
111 old_ep_item = self.EP[i]
112 old_fx = self.EP_fx[i]
113 # old_fx = self.get_fx(old_ep_item)
114 a_b = True # 老支配行
115 b_a = True # 新支配老
116 for j in range(len(self.o_func.f_funcs)):
117 if old_fx[j] < new_dna_fx[j]:
118 b_a = False
119 if old_fx[j] > new_dna_fx[j]:
120 a_b = False
121 # T T : fx相等 直接不改變EP
122 # T F :老支配新 留老,一定不要新,結束循環.
123 # F T :新支配老 留新,一定不要這個老,繼續循環
124 # F F : 非支配關系 不操作,循環下一個
125 # TF為什麼結束循環,FT為什麼繼續循環,你們可以琢磨下
126 if a_b:
127 accept_new = False
128 break
129 if not a_b and b_a:
130 if len(self.EP) <= i:
131 print(len(self.EP), i)
132 del self.EP[i]
133 del self.EP_fx[i]
134 continue
135
136 if accept_new:
137 self.EP.append(new_dna)
138 self.EP_fx.append(new_dna_fx)
139 return self.EP, self.EP_fx
140
141 def update_Z(self, new_dna):
142 new_dna_fx = self.get_fx(new_dna)
143 Z = self.Z
144 for i in range(len(self.o_func.f_funcs)):
145 if new_dna_fx[i] < Z[i]:
146 Z[i] = new_dna_fx[i]
147 return Zimport random
import numpy as np
from GA.MOEAD.Moead_Util import Moead_Util
from GA.MOEAD.Objective_Function import Objective_Function
from GA.MOEAD.Person import Person
import matplotlib.pyplot as plt
def draw(x, y):
plt.scatter(x, y, s=10, c="grey") # s 點的大小 c 點的顏色 alpha 透明度
plt.show()
iterations = 1000 # 迭代次數
N = 400
m = 2
T = 40
o_func = Objective_Function.get_one_function("zdt3")
pm = 0.5
moead = Moead_Util(N, m, T, o_func, pm)
moead.init_mean_vector()
moead.init_Euler_distance()
pop = moead.init_population()
moead.init_Z()
for i in range(iterations):
print(i, len(moead.EP))
for person in pop:
p1, p2 = person.choice_two_person()
d1, d2 = Person.cross_get_two_new_dna(p1, p2)
if np.random.rand() < pm:
p1.mutation_dna(d1)
if np.random.rand() < pm:
p1.mutation_dna(d2)
moead.update_Z(d1)
moead.update_Z(d2)
t1, t2 = person.choice_two_person()
if t1.compare(d1) < 0:
t1.accept_new_dna(d1)
moead.update_ep(d1)
if t2.compare(d1) < 0:
t2.accept_new_dna(d2)
moead.update_ep(d1)
# 輸出結果畫圖
EP_fx = np.array(moead.EP_fx)
x = EP_fx[:, 0]
y = EP_fx[:, 1]
draw(x, y)