jdk源碼分析PriorityQueue，jdkpriorityqueue

jdk源碼分析PriorityQueue，jdkpriorityqueue

一、結構

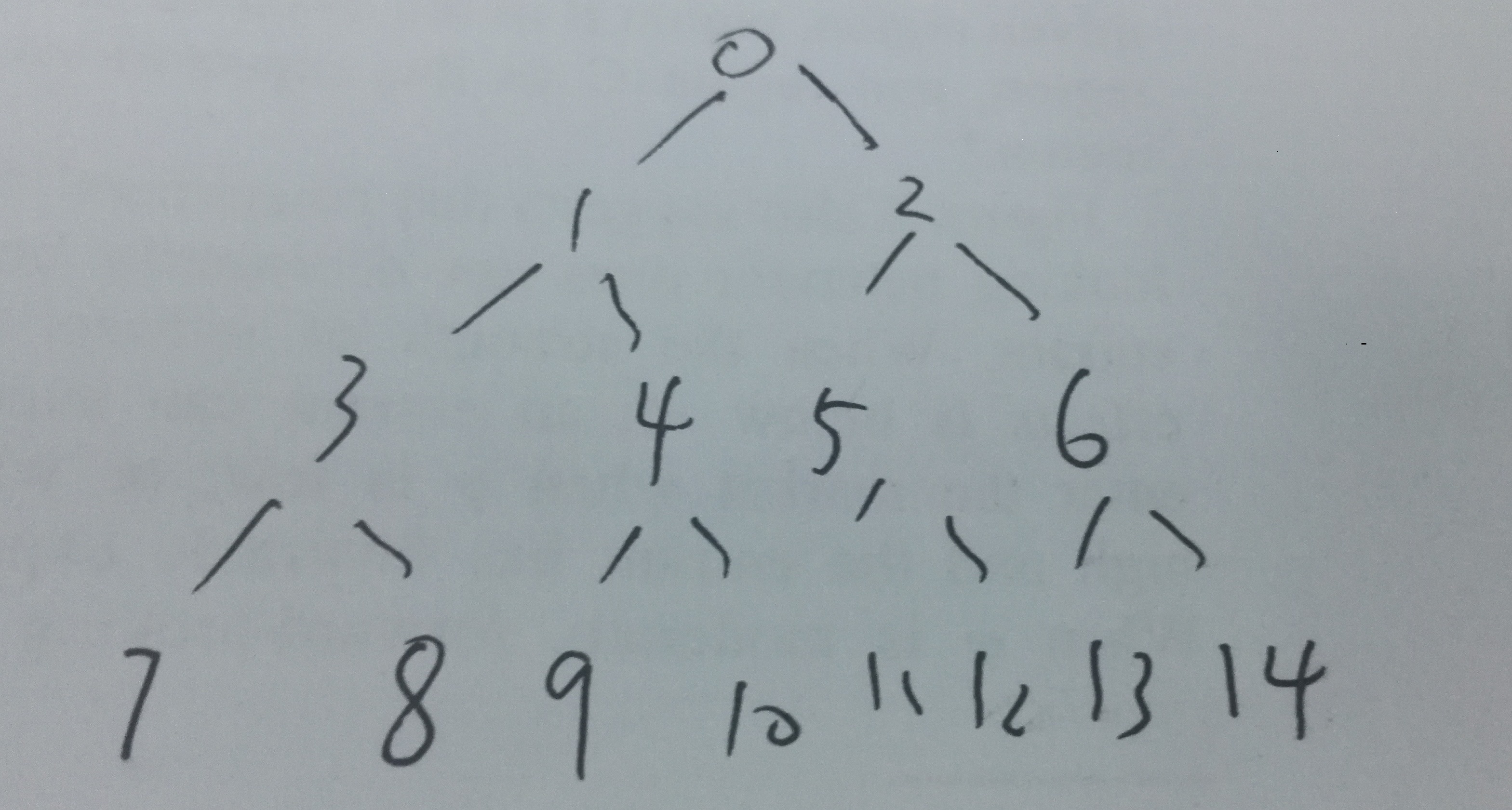
PriorityQueue是一個堆,任意節點都是以它為根節點的子樹中的最小節點 堆的邏輯結構是完全二叉樹狀的，存儲結構是用數組去存儲的，隨機訪問性好。最小堆的根元素是最小的，最大堆的根元素是最大的 這是一個最小堆的邏輯結構 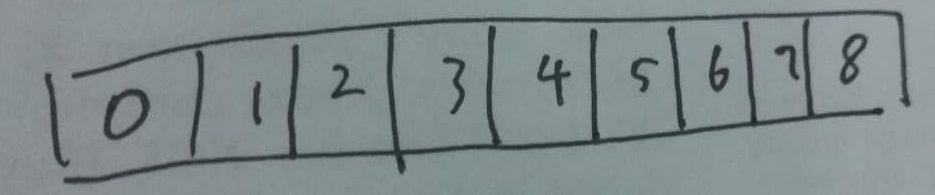這是他的存儲結構，是用數組來存儲的。 可以看到，i下標的數組元素，他的父節點是(i-1)/2，他的左右節點分別是i*2+1,i*2+2

二、容量

2.1初始容量11

2.2擴展容量

    private void grow(int minCapacity) {
        int oldCapacity = queue.length;
        // Double size if small; else grow by 50%
        int newCapacity = oldCapacity + ((oldCapacity < 64) ? (oldCapacity + 2) : (oldCapacity >> 1));
        // overflow-conscious code
        if (newCapacity - MAX_ARRAY_SIZE > 0)
            newCapacity = hugeCapacity(minCapacity);
        queue = Arrays.copyOf(queue, newCapacity);
    }

當容量不足的時候，會調用此方法，如果當前容量較小（小於64），則將容量增大一倍+2,如果當前容量較大，則容量增大一半

三、插入

插入元素會調用siftUp方法。

    private void siftUpComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>) x;
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (key.compareTo((E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = key;
    }

當優先隊列不指定比較器的時候，插入元素，會調用siftUpComparable k表示元素將要插入的位置 這個方法的意思是，在以k為子節點的子樹插入元素x，並保持該子樹的順序。（把k看作這個子樹的葉子節點） step1:得出父元素的下標 strp2:計算出要插入元素的位置k。如果插入元素大於父元素，將父元素移動到k的位置，k移動到其父元素，並從第一步開始循環執行 step3:在k的位置插入元素

四、刪除

    private void siftDownComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>)x;
        int half = size >>> 1;        // loop while a non-leaf
        while (k < half) {
            int child = (k << 1) + 1; // assume left child is least
            Object c = queue[child];
            int right = child + 1;
            if (right < size &&
                ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
                c = queue[child = right];
            if (key.compareTo((E) c) <= 0)
                break;
            queue[k] = c;
            k = child;
        }
        queue[k] = key;
    }

刪除會調用這個方法。刪除都是將隊尾的元素替換掉刪除掉的位置 k表示元素將要插入的位置 這個方法的意思是，在k的子樹插入元素x，並保持k位置子樹的順序（x是其子樹的最小節點）。（把k看作這個子樹的根節點） 這裡要注意，像這種二叉樹結構，下標大於size<<2都是葉子節點，其他的節點都有子節點。所以注意到循環條件，如果k是葉子節點的下標，則直接替換，因為其已經沒有子樹了，那麼肯定是以其為根節點的最小元素 step1:算出k的左右節點的下標 step2:如果k大於左右節點中的最小一個，則k與最小的節點互換位置，並循環step1 step3:在k位置賦值x

查看原文：http://blog.zswlib.com/2016/10/31/jdk%e6%ba%90%e7%a0%81%e5%88%86%e6%9e%90priorityqueue/