杭電acm5698-瞬間移動(2016"百度之星"，杭電acm5698-

杭電acm5698-瞬間移動(2016"百度之星"，杭電acm5698-

題目地址：http://acm.hdu.edu.cn/showproblem.php?pid=5698

Problem Description

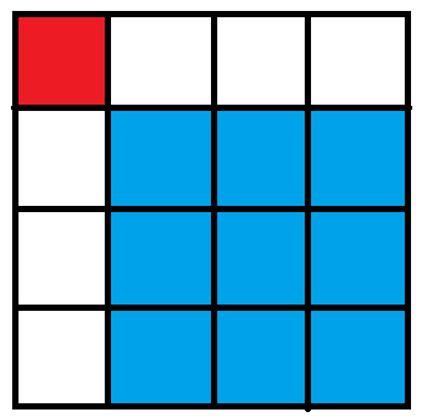
有一個無限大的矩形，初始時你在左上角（即第一行第一列），每次你都可以選擇一個右下方格子，並瞬移過去（如從下圖中的紅色格子能直接瞬移到藍色格子），求到第nnn行第mmm列的格子有幾種方案，答案對100000000710000000071000000007取模。

多組測試數據。

兩個整數n,m(2≤n,m≤100000)n,m(2\leq n,m\leq 100000)n,m(2≤n,m≤100000)

一個整數表示答案

/*
#include<stdio.h>
#include<stdlib.h>
int a[300][300]={0};
int main()
{
    int n,m,i,j; 
    //printf("%d\n",a[1][1]);
    for (i=2;i<300;i++)
    {
        a[i][2] = 1;
        a[2][i] = 1;
    }
    for (i=3;i<300;i++)
    {
        for (j=3;j<300;j++)
        {
            a[i][j] = a[i][j-1]+a[i-1][j];
            a[i][j] = a[i][j]%1000000007;
        }
    }
    while (scanf("%d%d",&n,&m)!=EOF)
    {
        printf("%d\n",a[n][m]);
    }
    return 0;
}
*/

//ac代碼
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#include<stack>
#include<map>
#define ll __int64
#define mod 1000000007
using namespace std;
ll poww(ll a,ll n)
{
   ll r=1,p=a;
   while(n)
   {
       if(n&1) r=(r*p)%mod;
       n>>=1;
       p=(p*p)%mod;
   }
   return r;
}
ll coun(ll n,ll m) 
{
    ll sum=1; 
    for(ll i=1,j=n;i<=m;i++,j--)
    {
        sum*=j;
        sum%=mod;
        sum*=poww(i,1000000005);
        sum%=mod;
    }
    return sum;
}
 ll x,y,z,t; 
 ll n,k;
 ll ans;
int main()
{
    while(scanf("%I64d %I64d",&x,&y)!=EOF)
    {
        ans=0;
        n=(x+y)-4;
        k=x-2;
        ans=coun(n,k);
        cout<<ans<<endl;
    }
    return 0;
}



/*
//ac代碼
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<queue>
#include<algorithm>
#include<stack>
#include<cstring>
#include<vector>
#include<list>
#include<set>
#include<map>
using namespace std;
#define ll long long
#define mod 1000000007
#define inf 999999999
#define pi 4*atan(1)
//#pragma comment(linker, "/STACK:102400000,102400000")
int scan()
{
    int res = 0 , ch ;
    while( !( ( ch = getchar() ) >= '0' && ch <= '9' ) )
    {
        if( ch == EOF ) return 1 << 30 ;
    }
    res = ch - '0' ;
    while( ( ch = getchar() ) >= '0' && ch <= '9' )
        res = res * 10 + ( ch - '0' ) ;
    return res ;
}
void extend_Euclid(ll a, ll b, ll &x, ll &y)
{
    if(b == 0)
    {
        x = 1;
        y = 0;
        return;
    }
    extend_Euclid(b, a % b, x, y);
    ll tmp = x;
    x = y;
    y = tmp - (a / b) * y;
}
ll combine1(ll n,ll m) //計算組合數C(n,m)
{
    ll sum=1; //線性計算
    for(ll i=1,j=n;i<=m;i++,j--)
    {
        sum*=j;
        sum%=mod;
        ll x,y;
        extend_Euclid(i,mod,x,y);
        sum*=(x%mod+mod)%mod;
        sum%=mod;
    }
    return sum;
}
int main()
{
    ll x,y,z,i,t;
    while(~scanf("%I64d%I64d",&x,&y))
    {
        ll n,k;
        ll ans=0;
        k=x-2;
        n=(x+y)-4;
        ans=combine1(n,k);
        printf("%I64d\n",ans);
    }
    return 0;
}

*/