在二叉樹的一些應用中,常常要求在樹中查找具有某種特征的結點,或者對樹中全部結點逐一進行某種處理。這就提出了一個遍歷二叉樹的問題,即如何按某條搜索路徑巡訪樹中的每個結點,使得每個結點均被訪問一次,而且僅被訪問一次。
由二叉樹的遞歸定義可知,二叉樹是由三個基本單元構成的:根結點,左子樹和右子樹。若能依次遍歷這三部分,便是遍歷了整個二叉樹。若限定先左後右的順序,則遍歷二叉樹通常有三種算法:先序,中序,後序。
先序遍歷二叉樹的操作定義為:
若二叉樹為空,則空操作;否則;
(1)訪問根結點;(2)先序遍歷左子樹;(3)先序遍歷右子樹。
中序遍歷二叉樹的操作定義為:
若二叉樹為空,則空操作;否則;
(1)中序遍歷左子樹;(2)訪問根結點;(3)中序遍歷右子樹。
後序遍歷二叉樹的操作定義為:若二叉樹為空,則空操作;否則;
(1)後序遍歷左子樹;(2)後序遍歷右子樹;(3)訪問根結點。
對於二叉樹的遍歷我們在二叉樹的二叉鏈表上實現。在二叉樹的二叉鏈表的基本操作中也介紹了四種遍歷方法,我們就來實現前三種遍歷方法。在遍歷函數的參數中除了一個指針參數外,還有一個指向函數的指針參數。這個函數最簡單的實現為Visit()函數。這個函數最簡單的代碼為:
Status printElement(TElemType e)//最簡單的Visit()函數
{
cout< 再者就是需要構建二叉表(先序輸入數據元素)的代碼:
Status CreateBiTree(BiTree &T)//按先序次序輸入二叉樹中結點的值(一個字符),空格字符表示空樹,構造二叉鏈表表示的二叉樹T
{
int i=0;
char a[100];
cin>>a[i];
if(a[i]=='#') T=NULL;
else
{
if(!(T=(BiTNode *)malloc(sizeof(BiTNode))))
{
exit(OVERFLOW);
}
T->data=a[i];//生成根結點
CreateBiTree(T->lchild); //構造左子樹
CreateBiTree(T->rchild); //構造右子樹
}
return OK;
}
先來看看二叉鏈表的先序遍歷代碼:
Status PreOrderTraverse(BiTree T, Status(*Visit)(TElemType e))//先序遍歷二叉樹
{
if(T)
{
if(Visit(T->data))
{
if(PreOrderTraverse(T->lchild,Visit))
{
if(PreOrderTraverse(T->rchild,Visit))
{
return OK;
}
}
return ERROR;
}
}
else
{
return OK;
}
}
再來看二叉鏈表的中序遍歷代碼:
Status InOrderTraverse(BiTree T, Status(*Visit)(TElemType e))//中序遍歷二叉樹
{
if(T)
{
if(InOrderTraverse(T->lchild,Visit))
{
if(Visit(T->data))
{
if(InOrderTraverse(T->rchild,Visit))
{
return OK;
}
}
return ERROR;
}
}
else
{
return OK;
}
}
最後來看二叉鏈表的後序遍歷代碼:
Status PostOrderTraverse(BiTree T, Status(*Visit)(TElemType e))//後序遍歷二叉樹
{
if(T)
{
if(PostOrderTraverse(T->lchild,Visit))
{
if(PostOrderTraverse(T->rchild,Visit))
{
if(Visit(T->data))
{
return OK;
}
}
return ERROR;
}
}
else
{
return OK;
}
}
完整的代碼為:
#include
#include
using namespace std;
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef char TElemType;
typedef int Status;
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild,*rchild; //左右孩子指針
}BiTNode,*BiTree;
Status CreateBiTree(BiTree &T)//按先序次序輸入二叉樹中結點的值(一個字符),空格字符表示空樹,構造二叉鏈表表示的二叉樹T
{
int i=0;
char a[100];
cin>>a[i];
if(a[i]=='#') T=NULL;
else
{
if(!(T=(BiTNode *)malloc(sizeof(BiTNode))))
{
exit(OVERFLOW);
}
T->data=a[i];//生成根結點
CreateBiTree(T->lchild); //構造左子樹
CreateBiTree(T->rchild); //構造右子樹
}
return OK;
}
Status PreOrderTraverse(BiTree T, Status(*Visit)(TElemType e))//先序遍歷二叉樹
{
if(T)
{
if(Visit(T->data))
{
if(PreOrderTraverse(T->lchild,Visit))
{
if(PreOrderTraverse(T->rchild,Visit))
{
return OK;
}
}
return ERROR;
}
}
else
{
return OK;
}
}
Status InOrderTraverse(BiTree T, Status(*Visit)(TElemType e))//中序遍歷二叉樹
{
if(T)
{
if(InOrderTraverse(T->lchild,Visit))
{
if(Visit(T->data))
{
if(InOrderTraverse(T->rchild,Visit))
{
return OK;
}
}
return ERROR;
}
}
else
{
return OK;
}
}
Status PostOrderTraverse(BiTree T, Status(*Visit)(TElemType e))//後序遍歷二叉樹
{
if(T)
{
if(PostOrderTraverse(T->lchild,Visit))
{
if(PostOrderTraverse(T->rchild,Visit))
{
if(Visit(T->data))
{
return OK;
}
}
return ERROR;
}
}
else
{
return OK;
}
}
Status printElement(TElemType e)//最簡單的Visit()函數
{
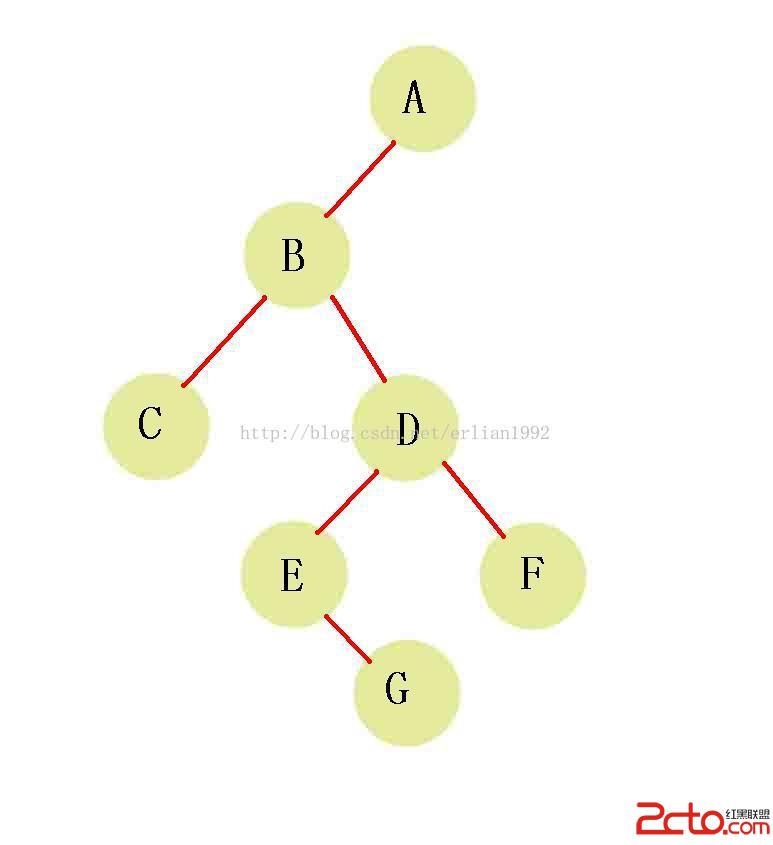
cout< 輸入的數據:先序輸入ABC##DE#G##F###(#代表空)
這棵樹的圖為:
輸出的結果為: