問題描述:
在一個2^k×2^k個方格組成的棋盤中,若有一個方格與其他方格不同,則稱該方格為一特殊方格,且稱該棋盤為一個特殊棋盤.顯然特殊方格在棋盤上出現的位置有4^k種情形.因而對任何k≥0,有4^k種不同的特殊棋盤.
下圖–圖(1)中的特殊棋盤是當k=3時16個特殊棋盤中的一個:
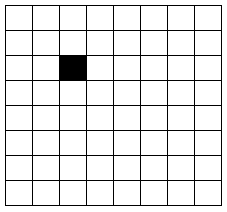
圖(1)
題目要求在棋盤覆蓋問題中,要用下圖-圖(2)所示的4種不同形態的L型骨牌覆蓋一個給定的特殊棋盤上除特殊方格以外的所有方格,且任何2個L型骨牌不得重疊覆蓋.
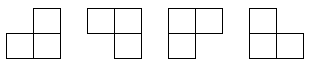
圖(2)
題目包含多組測試數據,輸入包含測試數據組數N,下面輸入N組數據,每組數據,包括邊長m和特殊方格的位置x,y。
input sample
2
2
0 0
8
2 2
output sample
CASE:1
0 1
1 1
CASE:2
3 3 4 4 8 8 9 9
3 2 2 4 8 7 7 9
5 2 0 6 10 10 7 11
5 5 6 6 1 10 11 11
13 13 14 1 1 18 19 19
13 12 14 14 18 18 17 19
15 12 12 16 20 17 17 21
15 15 16 16 20 20 21 21
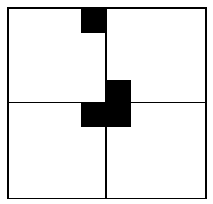
題解:當 k>0 時,將 2^k * 2^k 棋盤分割為 4 個 2^(k-1) * 2^(k-1) 子棋盤,如下圖所示。

特殊方格必位於 4 個較小子棋盤之一中,其余 3 個子棋盤中無特殊方格。為了將這 3 個無特殊方格的子棋盤轉化為特殊棋盤,我們可以用一個 L 型骨牌覆蓋這 3 個較小的棋盤的匯合處,如下圖所示,這 3 個子棋盤上被 L 型骨牌覆蓋的方格就成為該棋盤上的特殊方格,從而將原問題化為 4 個較小規模的棋盤覆蓋問題。遞歸的使用 這種分割,直至棋盤簡化為 1x1 棋盤。
#include<iostream>
using namespace std;
int tile=1; //L型骨牌的編號(遞增)
int b[100][100]; //棋盤
/*****************************************************
* 遞歸方式實現棋盤覆蓋算法
* 輸入參數:
* tr--當前棋盤左上角的行號
* tc--當前棋盤左上角的列號
* dr--當前特殊方格所在的行號
* dc--當前特殊方格所在的列號
* size:當前棋盤的:2^k
*****************************************************/
void chessBoard ( int tr, int tc, int dr, int dc, int size )
{
if ( size==1 ) //棋盤方格大小為1,說明遞歸到最裡層
return;
int t=tile++; //每次遞增1
int s=size/2; //棋盤中間的行、列號(相等的)
//檢查特殊方塊是否在左上角子棋盤中
if ( dr<tr+s && dc<tc+s ) //在
chessBoard ( tr, tc, dr, dc, s );
else //不在,將該子棋盤右下角的方塊視為特殊方塊
{
b[tr+s-1][tc+s-1]=t;
chessBoard ( tr, tc, tr+s-1, tc+s-1, s );
}
//檢查特殊方塊是否在右上角子棋盤中
if ( dr<tr+s && dc>=tc+s ) //在
chessBoard ( tr, tc+s, dr, dc, s );
else //不在,將該子棋盤左下角的方塊視為特殊方塊
{
b[tr+s-1][tc+s]=t;
chessBoard ( tr, tc+s, tr+s-1, tc+s, s );
}
//檢查特殊方塊是否在左下角子棋盤中
if ( dr>=tr+s && dc<tc+s ) //在
chessBoard ( tr+s, tc, dr, dc, s );
else //不在,將該子棋盤右上角的方塊視為特殊方塊
{
b[tr+s][tc+s-1]=t;
chessBoard ( tr+s, tc, tr+s, tc+s-1, s );
}
//檢查特殊方塊是否在右下角子棋盤中
if ( dr>=tr+s && dc>=tc+s ) //在
chessBoard ( tr+s, tc+s, dr, dc, s );
else //不在,將該子棋盤左上角的方塊視為特殊方塊
{
b[tr+s][tc+s]=t;
chessBoard ( tr+s, tc+s, tr+s, tc+s, s );
}
}
int main()
{
int t,size,x,y,total=0;
cin>>t;
while(t--)
{
cin>>size;
cin>>x>>y;
total++;
chessBoard (0,0,x,y,size );
cout<<"CASE:"<<total<<endl;
for ( int i=0; i<size; i++ )
{
for ( int j=0; j<size; j++ )
cout<<b[i][j]<<" ";
cout<<endl;
}
}
}