這篇文章是對《算法導論》上Prim算法求無向連通圖最小生成樹的一個總結,其中有關於我的一點點小看法。
最小生成樹的具體問題可以用下面的語言闡述:
輸入:一個無向帶權圖G=(V,E),對於每一條邊(u, v)屬於E,都有一個權值w。
輸出:這個圖的最小生成樹,即一棵連接所有頂點的樹,且這棵樹中的邊的權值的和最小。
舉例如下,求下圖的最小生成樹:
兩科子樹T1和T2,如圖:
1 #include <iostream>
2 #include <cstdio>
3 #include <vector>
4 #include <queue>
5 using namespace std;
6
7 #define maxn 110 //最大頂點個數
8 int n, m; //頂點數,邊數
9
10 struct arcnode //邊結點
11 {
12 int vertex; //與表頭結點相鄰的頂點編號
13 int weight; //連接兩頂點的邊的權值
14 arcnode * next; //指向下一相鄰接點
15 arcnode() {}
16 arcnode(int v,int w):vertex(v),weight(w),next(NULL) {}
17 };
18
19 struct vernode //頂點結點,為每一條鄰接表的表頭結點
20 {
21 int vex; //當前定點編號
22 arcnode * firarc; //與該頂點相連的第一個頂點組成的邊
23 }Ver[maxn];
24
25 void Init() //建立圖的鄰接表需要先初始化,建立頂點結點
26 {
27 for(int i = 1; i <= n; i++)
28 {
29 Ver[i].vex = i;
30 Ver[i].firarc = NULL;
31 }
32 }
33
34 void Insert(int a, int b, int w) //尾插法,插入以a為起點,b為終點,權為w的邊,效率不如頭插,但是可以去重邊
35 {
36 arcnode * q = new arcnode(b, w);
37 if(Ver[a].firarc == NULL)
38 Ver[a].firarc = q;
39 else
40 {
41 arcnode * p = Ver[a].firarc;
42 if(p->vertex == b)
43 {
44 if(p->weight > w)
45 p->weight = w;
46 return ;
47 }
48 while(p->next != NULL)
49 {
50 if(p->next->vertex == b)
51 {
52 if(p->next->weight > w);
53 p->next->weight = w;
54 return ;
55 }
56 p = p->next;
57 }
58 p->next = q;
59 }
60 }
61
62 struct node //保存key值的結點
63 {
64 int v;
65 int key;
66 friend bool operator<(node a, node b) //自定義優先級,key小的優先
67 {
68 return a.key > b.key;
69 }
70 };
71
72 #define INF 0xfffff //權值上限
73 int parent[maxn]; //每個結點的父節點
74 bool visited[maxn]; //是否已經加入樹種
75 node vx[maxn]; //保存每個結點與其父節點連接邊的權值
76 priority_queue<node> q; //優先隊列stl實現
77 void Prim(int s) //s表示根結點
78 {
79 for(int i = 1; i <= n; i++) //初始化
80 {
81 vx[i].v = i;
82 vx[i].key = INF;
83 parent[i] = -1;
84 visited[i] = false;
85 }
86 vx[s].key = 0;
87 q.push(vx[s]);
88 while(!q.empty())
89 {
90 node nd = q.top(); //取隊首,記得趕緊pop掉
91 visited[nd.v] = true;
92 q.pop();
93 arcnode * p = Ver[nd.v].firarc;
94 while(p != NULL) //找到所有相鄰結點,若未訪問,則入隊列
95 {
96 if(!visited[p->vertex] && p->weight < vx[p->vertex].key)
97 {
98 parent[p->vertex] = nd.v;
99 vx[p->vertex].key = p->weight;
100 vx[p->vertex].v = p->vertex;
101 q.push(vx[p->vertex]);
102 }
103 p = p->next;
104 }
105 }
106 }
107
108 int main()
109 {
110 int a, b ,w;
111 cout << "輸入n和m: ";
112 cin >> n >> m;
113 Init();
114 cout << "輸入所有的邊:" << endl;
115 while(m--)
116 {
117 cin >> a >> b >> w;
118 Insert(a, b, w);
119 Insert(b, a, w);
120 }
121 Prim(1);
122 cout << "輸出所有結點的父結點:" << endl;
123 for(int i = 1; i <= n; i++)
124 cout << parent[i] << " ";
125 cout << endl;
126 cout << "最小生成樹權值為:";
127 int cnt = 0;
128 for(int i = 1; i <= n; i++)
129 cnt += vx[i].key;
130 cout << cnt << endl;
131 return 0;
132 }
View Code
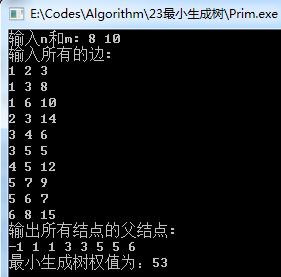
運行結果如下(基於第一個例子):
望支持,謝謝。