牛頓迭代公式
設已知方程f(x)=0的近似根x0 ,則在x0附近f(x)可用一階泰勒多項式近似代替.因此, 方程f(x)=0可近似地表示為p(x)=0。用x1表示p(x)=0的根,它與f(x)=0的根差異不大.
設 ,由於x1滿足解得
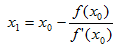重復這一過程,得到迭代公式：
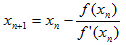這就是著名的牛頓迭代公式,它相應的不動點方程為
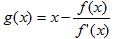Jacobi迭代公式解線性方程組
線性方程組基本解法：
若方程組可同解變形為
Jacobi迭代法的計算公式：
即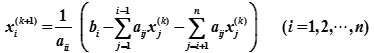 
算法代碼
[cpp]
/*簡單迭代法的代碼實現*/
#include<iostream>
#include<string>
#include<cmath>
using namespace std;
double e=2.718281818284;
double f(double x){
return pow(e,-1*x);
}
void SimpleDiedai(double x,double d){
double a=x;
double b=f(a);
int k=0;//記錄循環的次數
while(((a-b)>d) || ((a-b)<-1*d)){
cout<<a<<endl;
a=b;
b=f(a);
k++;
if(k>100){
cout<<"迭代失敗！（可能是函數不收斂）"<<endl;
return ;
}
}
cout<<b<<endl;
return;
}
int main(){
cout<<"請輸入初始值x0和要求得結果的精度：";
double x,d;
cin>>x>>d;
SimpleDiedai (x,d);
return 0;
} www.2cto.com
/*牛頓迭代法的代碼實現*/
#include<iostream>
#include<string>
#include<cmath>
using namespace std;
double e=2.718281818284;
double f(double x){
double a=pow(e,-1*x);
return x-(x-a)/(1+a);
}
void NewtonDiedai(double x,double d){
double a=x;
double b=f(a);
int k=0; //記錄循環的次數
while(((a-b)>d) || ((a-b)<-1*d)){
cout<<a<<endl;
a=b;
b=f(a);
k++;
if(k>100){
cout<<"迭代失敗！（可能是函數不收斂）"<<endl;
return ;
}
}
cout<<b<<endl;
return;
}
int main(){
cout<<"請輸入初始值x0和要求得結果的精度：";
double x,d;
cin>>x>>d;
NewtonDiedai(x,d);
return 0;
}
/*雅可比算法的代碼實現*/
#include<iostream>
#include<iomanip>
#include<string>
#include<vector>
using namespace std;
//函數求數組中的最大值
double MaxOfList(vector<double>x){
double max=x[0];
int n=x.size();
for(int i=0;i<n;i++)
if(x[i]>max) max=x[i];
return max;
}
//雅可比迭代公式
void Jacobi(vector<vector<double> > A,vector<double> B,int n){
vector<double> X(n,0);
vector<double> Y(n,0);
vector<double> D(n,0);
int k=0; //記錄循環次數
do{
X=Y;
for(int i=0;i<n;i++){
double tem=0;
for(int j=0;j<n;j++){
if(i!=j) tem += A[i][j]*X[j];
}
Y[i]=(B[i]-tem)/A[i][i];
cout<<left<<setw(8)<<Y[i]<<" ";
}
cout<<endl;
k++;
if(k>100){
cout<<"迭代失敗！（可能是函數不收斂）"<<endl;
return ;
}
for(int a=0;a<n;a++){
D[a]=X[a]-Y[a];
}
}while( MaxOfList(D)>0.00001 || MaxOfList(D)<-0.00001);
return ;
}
int main(){
int n;
cout<<"請輸入方程組未知數的個數n：";
cin>>n;
cout<<endl;
vector<vector<double> >A(n,vector<double>(n,0));
vector<double>B(n,0);
cout<<"請輸入方程組的系數矩陣："<<endl;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>A[i][j];
}
}
cout<<endl;
cout<<"請輸入方程組的值向量："<<endl;
for(int k=0;k<n;k++){
cin>>B[k];
}
cout<<endl;
cout<<"您輸入的方程組為："<<endl;
for(int a=0;a<n;a++){
for(int b=0;b<n;b++){
cout<<A[a][b]<<" ";
}
cout<<" "<<B[a]<<endl;
}
cout<<endl;
cout<<"由雅可比迭代公式求的方程組的解為："<<endl;
Jacobi(A,B,n);
return 0;
}
實驗過程原始記錄
（1）分別用簡單迭代法和牛頓迭代法求方程在x=0.5附近的一個根x*，要求精度為0.00001
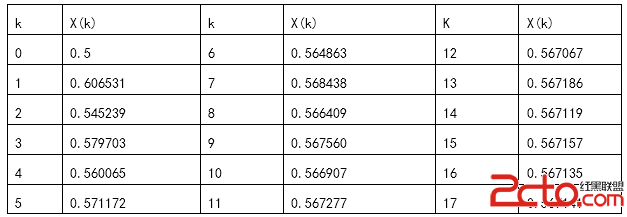
（輸入0.5 0.000001）簡單迭代法得到結果：
（輸入0.5 0.000001）牛頓迭代法得到結果：
X0=0.5 x1=0.566311 x2=0.567143
（2）用雅可比迭代法求解方程組
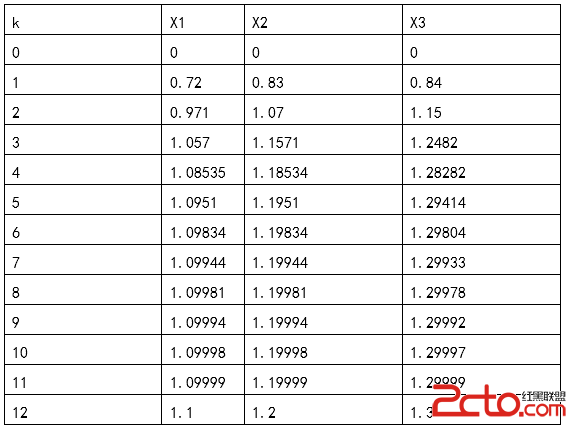
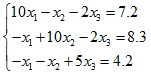運行程序，根據提示輸入 （3） （10 -1 -2 -1 10 -2 -1 -2 5） （7.2 8.3 4.2）
實驗結果及分析
1、迭代法是一種逐次逼近法，這種方法使用某個固定公式－所謂迭代公式反復校正根的近似值，使之逐步精確化，直至滿足精度要求的結果。迭代法是一種求解函數方程f（x）=0的解的方法，他解決了二分法無法求解復根級偶重根的問題，而其提高了收斂速度。迭代的思想是計算方法中基礎的求解問題的思想。
2、簡單迭代法的求根過程分成兩步，第一步先提供根的某個猜測值，即所謂迭代初值，然後將迭代初值逐步加工成滿足精度要求的根。迭代法的設計思想是：f (x) = 0等價變換成 然後由迭代公式 逐步球的滿足精度的解。實際迭代中不同迭代函數的求解可能影響求的精確解的運算量，甚至可能因為函數發散而無法求解。解題時可通過對導函數的判斷而判斷函數是否發散，而編寫代碼時可以通過判斷循環次數——即循環過多次而不能從循環中出來時就判斷為死循環，無法求得正解
3、簡單迭代法往往只是線性收斂，為得出超線性收斂的迭代格式，通常采用近似替代法， 即牛頓公式。迭代函數為 - / 牛頓法是一種逐步線性化方法。由實驗結果可以看到，雖然選取近似公式，但牛頓迭代法仍能得到精度很高的解，而且牛頓迭代法大大提高了收斂速度。
4、由迭代法求解線性方程組的基本思想是將聯立方程組的求解歸結為重復計算一組彼此獨立的線性表達式，這就使問題得到了簡化，類似簡單迭代法轉換方程組中每個方程式可得到雅可比迭代式
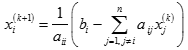迭代法求解方程組有一定的局限性，例如要求方程組的系數矩陣具有某種特殊性質，以保證迭代過程的收斂性，但迭代法同時有十分明顯的優點——算法簡單，因而編制程序比較容易，所以在實際求解問題中仍有非常大利用價值。
