我用DEV-C++測過用例,通過了,可是提交到PAT上全都是段錯誤,今天是沒辦法了。花了一整天,叫我寫點關於解這題的心得,抱歉,頭痛。
1 #include <stdio.h>
2 #include <stdlib.h>
3 #include <stdbool.h>
4 #include <string.h>
5
6 typedef struct node
7 {
8 int v;
9 struct node * next;
10 }Node, * pNode;
11 typedef struct
12 {
13 pNode * adjList;
14 int n;
15 bool * visited;
16 }ALGraph, * pALGraph;
17 typedef struct
18 {
19 int * elem;
20 int front, rear, size;
21 }Queue, * pQueue;
22
23 pALGraph initGraph(int N);
24 void link(pALGraph pG, int v1, int v2);
25 void insert(pNode pN, int vv);
26 int BFS(pALGraph, int vv, int N);
27 pQueue createQueue(int N);
28 bool isEmpty(pQueue pQ);
29 void inQueue(pQueue pQ, int e);
30 int outQueue(pQueue pQ);
31
32 int main()
33 {
34 // freopen("in.txt", "r", stdin); // for test
35 int i, N, M;
36 scanf("%d%d", &N, &M);
37
38 pALGraph pG;
39 pG = initGraph(N);
40 for(i = 0; i < M; i++)
41 {
42 int v1, v2;
43 scanf("%d%d", &v1, &v2);
44 link(pG, v1, v2);
45 }
46 int count;
47 for(i = 1; i <= N; i++)
48 {
49 count = BFS(pG, i, N);
50 printf("%d: %.2f%%\n", i, (float)count / N * 100);
51 }
52 // fclose(stdin); // for test
53 return 0;
54 }
55
56 pALGraph initGraph(int N)
57 {
58 pALGraph pG;
59 pG = (pALGraph)malloc(sizeof(ALGraph));
60 pG->adjList = (pNode *)malloc((N + 1) * sizeof(pNode));
61 pG->n = N + 1;
62 pG->visited = (bool *)malloc((N + 1) * sizeof(bool));
63 memset(pG->visited, false, (N + 1) * sizeof(bool));
64 for(int i = 0; i < N + 1; i++)
65 {
66 pG->adjList[i] = (pNode)malloc(sizeof(Node));
67 pG->adjList[i]->v = i;
68 pG->adjList[i]->next = NULL;
69 }
70
71 return pG;
72 }
73
74 void link(pALGraph pG, int v1, int v2)
75 {
76 insert(pG->adjList[v1], v2);
77 insert(pG->adjList[v2], v1);
78 }
79
80 void insert(pNode pN, int vv)
81 {
82 pNode tmp = (pNode)malloc(sizeof(Node));
83 tmp->v = vv;
84 tmp->next = pN->next;
85 pN->next = tmp;
86 // free(tmp);
87 }
88
89 int BFS(pALGraph pG, int vv, int N)
90 {
91 pQueue pQ;
92 pQ = createQueue(N);
93
94 int i, count, level, last, tail;
95 pG->visited[vv] = true;
96 count = 1;
97 level = 0;
98 last = vv;
99 inQueue(pQ, vv);
100 while(!isEmpty(pQ))
101 {
102 vv = outQueue(pQ);
103 pNode pN = pG->adjList[vv]->next;
104 while(pN)
105 {
106 if(!pG->visited[pN->v])
107 {
108 pG->visited[pN->v] = true;
109 count++;
110 inQueue(pQ, pN->v);
111 tail = pN->v;
112 }
113 pN = pN->next;
114 }
115 if(vv == last)
116 {
117 level++;
118 last = tail;
119 }
120 if(level == 6)
121 break;
122 }
123 memset(pG->visited, false, (N + 1) * sizeof(bool));
124
125 return count;
126 }
127
128 pQueue createQueue(int N)
129 {
130 pQueue pQ;
131 pQ = (pQueue)malloc(sizeof(Queue));
132 pQ->elem = (int *)malloc((N + 1) * sizeof(int));
133 pQ->front = pQ->rear = 0;
134 pQ->size = N + 1;
135 }
136
137 bool isEmpty(pQueue pQ)
138 {
139 if(pQ->front != pQ->rear)
140 return false;
141 else
142 return true;
143 }
144
145 void inQueue(pQueue pQ, int e)
146 {
147 pQ->rear = (pQ->rear + 1) % pQ->size;
148 pQ->elem[pQ->rear] = e;
149 }
150
151 int outQueue(pQueue pQ)
152 {
153 pQ->front = (pQ->front + 1) % pQ->size;
154 return pQ->elem[pQ->front];
155 }
“六度空間”理論又稱作“六度分隔(Six Degrees of Separation)”理論。這個理論可以通俗地闡述為:“你和任何一個陌生人之間所間隔的人不會超過六個,也就是說,最多通過五個人你就能夠認識任何一個陌生人。”如圖6.4所示。
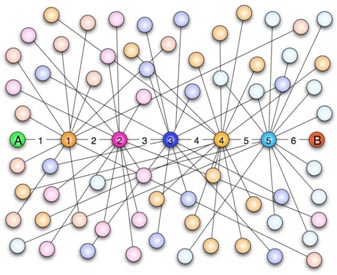
圖6.4 六度空間示意圖
“六度空間”理論雖然得到廣泛的認同,並且正在得到越來越多的應用。但是數十年來,試圖驗證這個理論始終是許多社會學家努力追求的目標。然而由於歷史的原因,這樣的研究具有太大的局限性和困難。隨著當代人的聯絡主要依賴於電話、短信、微信以及因特網上即時通信等工具,能夠體現社交網絡關系的一手數據已經逐漸使得“六度空間”理論的驗證成為可能。
假如給你一個社交網絡圖,請你對每個節點計算符合“六度空間”理論的結點占結點總數的百分比。
輸入格式說明:
輸入第1行給出兩個正整數,分別表示社交網絡圖的結點數N (1<N<=104,表示人數)、邊數M(<=33*N,表示社交關系數)。隨後的M行對應M條邊,每行給出一對正整數,分別是該條邊直接連通的兩個結點的編號(節點從1到N編號)。
輸出格式說明:
對每個結點輸出與該結點距離不超過6的結點數占結點總數的百分比,精確到小數點後2位。每個結節點輸出一行,格式為“結點編號:(空格)百分比%”。
樣例輸入與輸出:
序號 輸入 輸出 110 9 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10
1: 70.00% 2: 80.00% 3: 90.00% 4: 100.00% 5: 100.00% 6: 100.00% 7: 100.00% 8: 90.00% 9: 80.00% 10: 70.00%2
10 8 1 2 2 3 3 4 4 5 5 6 6 7 7 8 9 10
1: 70.00% 2: 80.00% 3: 80.00% 4: 80.00% 5: 80.00% 6: 80.00% 7: 80.00% 8: 70.00% 9: 20.00% 10: 20.00%3
11 10 1 2 1 3 1 4 4 5 6 5 6 7 6 8 8 9 8 10 10 11
1: 100.00% 2: 90.91% 3: 90.91% 4: 100.00% 5: 100.00% 6: 100.00% 7: 100.00% 8: 100.00% 9: 100.00% 10: 100.00% 11: 81.82%4
2 1 1 2
1: 100.00% 2: 100.00%