從第4節的分析中可以看出,二叉搜索樹是個很好的數據結構,可以快速地找到一個給定關鍵字的數據項,並且可以快速地插入和刪除數據項。但是二叉搜索樹有個很麻煩的問題,如果樹中插入的是隨機數據,則執行效果很好,但如果插入的是有序或者逆序的數據,那麼二叉搜索樹的執行速度就變得很慢。因為當插入數值有序時,二叉樹就是非平衡的了,它的快速查找、插入和刪除指定數據項的能力就喪失了。
2-3-4樹是一個多叉樹,它的每個節點最多有四個子節點和三個數據項。2-3-4樹和紅-黑樹一樣,也是平衡樹,它的效率比紅-黑樹稍差,但是編程容易。2-3-4樹名字中的2、3、4的含義是指一個節點可能含有的子節點的個數。對非葉節點有三種可能的情況:
·有一個數據項的節點總是有兩個子節點;
·有兩個數據項的節點總是有三個子節點;
·有三個數據項的節點總是有四個字節點。
簡而言之,非葉節點的子節點總是比它含有的數據項多1。如下圖所示:
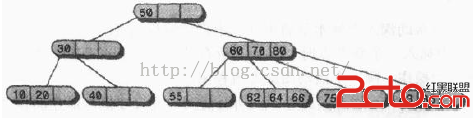
為了方便起見,用0到2給數據項編號,用0到3給子節點鏈編號。樹的結構中很重要的一點就是它的鏈與自己數據項的關鍵字值之間的關系。二叉樹所有關鍵字值比某個節點值小的都在這個節點的左子節點為根的子樹上,所有關鍵字值比某個及诶的那值大的節點都在這個節點右子節點為根的子樹上。2-3-4樹中規則是一樣的,還加上了以下幾點:
·根是child0的子樹的所有子節點的關鍵字值小於key0;
·根是child1的子樹的所有子節點的關鍵字值大於key0並且小於key1;
·根是child2的子樹的所有子節點的關鍵字值大於key1並且小於key2;
·根是child3的子樹的所有子節點的關鍵字值大於key2。
這種關系如下圖所示,2-3-4樹中一般不允許出現重復關鍵字值,所以不用考慮比較相同的關鍵字值的情況。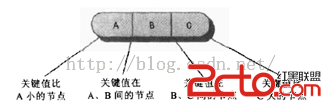
2-3-4樹中插入節點有時比較簡單,有時比較復雜。當沒有碰到滿節點時插入很簡單,找到合適的葉節點後,只要把新數據項插入進去即可,插入可能會涉及到在一個節點中移動一個或兩個其他的數據項,這樣在新的數據項插入後關鍵字值仍保持正確的順序。如下圖:
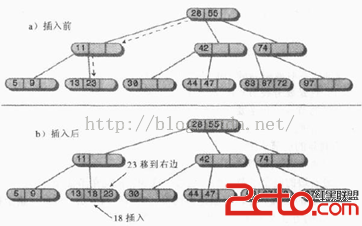
如果往下尋找要插入的位置的路途中,節點已經滿了,插入就變得復雜了。這種情況下,節點必須分裂。正是這種分裂過程保證了樹的平衡。設要分裂節點中的數據項為A、B、C,下面是分裂時的情況(假設分裂的節點不是根節點):
·創建一個新的空節點,它是要分裂節點的兄弟,在要分裂節點的右邊;
·數據項C移到新節點中;
·數據項B移動到要分裂節點的父節點中;
·數據項A保留在原來的位置;
·最右邊的兩個子節點從要分裂節點處斷開,連接到新節點上。
下圖顯示了一個節點分裂的過程。另一種描述節點分裂的方法是說4-節點變成了兩個2-節點。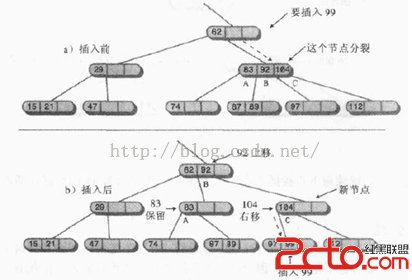
如果一開始查找插入點時就碰到滿根時,插入過程就更復雜一點:
·創建新的根。它是要分裂節點的父節點;
·創建第二個新的節點。它是要分裂節點的兄弟節點;
·數據項C移動到新的兄弟節點中;
·數據項B移動到新的根節點中;
·數據項A保留在原來的位置上;
·要分裂節點最右邊的兩個子節點斷開連接,連接到新的兄弟節點中。
下圖是根分裂的過程。過程中創建新的根,比舊的高一層,因此整個樹的高度就增加了一層。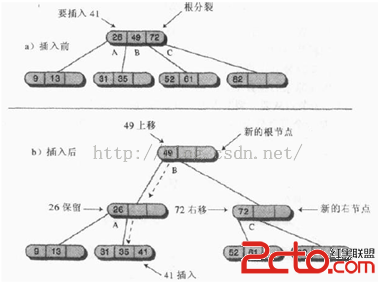
下面是2-3-4樹的代碼:
public class Tree234 {
private Node2 root = new Node2();
public int find(long key) {
Node2 currentNode = root;
int childNumber;
while(true) {
if((childNumber = currentNode.findItem(key)) != -1) {
return childNumber;
}
else if(currentNode.isLeaf()) {
return -1;
}
else {
currentNode = getNextChild(currentNode, key);
}
}
}
//insert a DataItem
public void insert(long data) {
Node2 currentNode = root;
DataItem tempItem = new DataItem(data);
while(true) {
if(currentNode.isFull()) {
split(currentNode); //if node is full, split it
currentNode = currentNode.getParent(); //back up
currentNode = getNextChild(currentNode, data); //search once
}
else if(currentNode.isLeaf()) { //if node if leaf
break; //go insert
}
else {
currentNode = getNextChild(currentNode, data);
}
}
currentNode.insertItem(tempItem);
}
//display tree
public void displayTree() {
recDisplayTree(root, 0, 0);
}
public Node2 getNextChild(Node2 currentNode, long key) {
int j;
//assumes node is not empty, not full and not leaf
int numItems = currentNode.getNumItems();
for(j = 0; j < numItems; j++) {
if(key < currentNode.getItem(j).dData) {
return currentNode.getChild(j);
}
}
return currentNode.getChild(j);
}
public void split(Node2 currentNode) {
//assumes node is full
DataItem itemB, itemC; //存儲要分裂節點的後兩個DataItem
Node2 parent, child2, child3; //存儲要分裂節點的父節點和後兩個child
int itemIndex;
itemC = currentNode.removeItem();
itemB = currentNode.removeItem(); //remove items from this node
child2 = currentNode.disconnectChild(2);
child3 = currentNode.disconnectChild(3); //remove children from this node
Node2 newRight = new Node2(); //make a new node
if(currentNode == root) {
root = new Node2(); //make a new root
parent = root; //root is our parent
root.connectChild(0, currentNode);//connect currentNode to parent
}
else {
parent = currentNode.getParent();
}
//deal with parent
itemIndex = parent.insertItem(itemB); //insert B to parent
int n = parent.getNumItems(); //total items
for(int j = n-1; j > itemIndex; j--) {
Node2 temp = parent.disconnectChild(j);
parent.connectChild(j+1, temp);
}
parent.connectChild(itemIndex+1, newRight);
//deal with newRight
newRight.insertItem(itemC);
newRight.connectChild(0, child2);
newRight.connectChild(1, child3);
}
public void recDisplayTree(Node2 thisNode, int level, int childNumber) {
System.out.print("level = " + level + " child = " + childNumber + " ");
thisNode.displayNode();
//call ourselves for each child of this node
int numItems = thisNode.getNumItems();
for(int j = 0; j < numItems+1; j++) {
Node2 nextNode = thisNode.getChild(j);
if(nextNode != null) {
recDisplayTree(nextNode, level+1, j);
}
else
continue;
}
}
}
//數據項
class DataItem {
public long dData;
public DataItem(long data) {
dData = data;
}
public void displayItem() {
System.out.print("/" + dData);
}
}
//節點
class Node2 {
private static final int ORDER = 4;
private int numItems; //表示該節點存有多少個數據項
private Node2 parent;
private Node2 childArray[] = new Node2[ORDER]; //存儲子節點的數組,最多四個子節點
private DataItem itemArray[] = new DataItem[ORDER-1];//該節點中存放數據項的數組,每個節點最多存放三個數據項
//連接子節點
public void connectChild(int childNum, Node2 child) {
childArray[childNum] = child;
if(child != null) {
child.parent = this;
}
}
//斷開與子節點的連接,並返回該子節點
public Node2 disconnectChild(int childNum) {
Node2 tempNode = childArray[childNum];
childArray[childNum] = null;
return tempNode;
}
public Node2 getChild(int childNum) {
return childArray[childNum];
}
public Node2 getParent() {
return parent;
}
public boolean isLeaf() {
return (childArray[0] == null);
}
public int getNumItems() {
return numItems;
}
public DataItem getItem(int index) {
return itemArray[index];
}
public boolean isFull() {
return (numItems == ORDER-1);
}
public int findItem(long key) {
for(int j = 0; j < ORDER-1; j++) {
if(itemArray[j] == null) {
break;
}
else if(itemArray[j].dData == key) {
return j;
}
}
return -1;
}
public int insertItem(DataItem newItem) {
//assumes node is not full
numItems++;
long newKey = newItem.dData;
for(int j = ORDER-2; j >= 0; j--) { //start on right
if(itemArray[j] == null) { //item is null
continue; //get left one cell
}
else { //not null
long itsKey = itemArray[j].dData; //get its key
if(newKey < itsKey) { //if it's bigger
itemArray[j+1] = itemArray[j]; //shift it right
}
else {
itemArray[j+1] = newItem; //insert new item
return j+1; //return index to new item
}
}
}
itemArray[0] = newItem;
return 0;
}
public DataItem removeItem() {
//assumes node not empty
DataItem tempItem = itemArray[numItems-1]; //save item
itemArray[numItems-1] = null; //disconnect it
numItems--;
return tempItem;
}
public void displayNode() {
for(int i = 0; i < numItems; i++) {
itemArray[i].displayItem();
}
System.out.println("/");
}
}
和紅-黑樹一樣,2-3-4樹同樣要訪問每層的一個節點,但2-3-4樹有比相同數據項的紅-黑樹短(層數少)。更特別的是,2-3-4樹中每個節點最多可以有4個子節點,如果每個節點都是滿的,樹的高度應該和log4N成正比。以2為底的對數和以4為底的對數底數相差2,因此,在所有節點都滿的情況下,2-3-4樹的高度大致是紅-黑樹的一般。不過它們不可能都是滿的,2-3-4樹的高度就大致在log2(N+1)和log2(N+1)/2之間。
另一方面,每個節點要查看的數據項就更多了,這會增加查找時間。因為節點中用線性搜索來查看數據項,使查找時間增加的倍數和M成正比,即每個節點數據項的平均數量。總的查找時間和M*log4N成正比。有些節點有1個數據項,有些有2個,有些有3個,如果按照平均兩個來計算,查找時間和2*log4N成正比。
因此,2-3-4樹中增加每個節點的數據項數量可以抵償樹的高度的減少。2-3-4樹中的查找時間與平衡二叉樹(如紅-黑樹)大致相等,都是O(logN)。