我們將研究兩種對分布進行抽樣的方法:拒絕抽樣和使用 Metropolis Hastings 算法的馬爾可夫鏈蒙特卡洛方法 (MCMC)。像往常一樣,我將提供直觀的解釋、理論和一些帶有代碼的示例。
在我們進入主題之前,讓我們將馬爾可夫鏈蒙特卡羅(MCMC)這個術語分解為它的基本組成部分:蒙特卡羅方法和馬爾可夫鏈。
Markov Chain 是“在狀態空間上經歷從一種狀態到另一種狀態的轉換的隨機過程”。
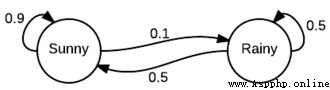
正如你所看到的,它看起來就像一個有限狀態機,只是我們用概率注釋了狀態轉換。例如,我們可以查看今天是否晴天,明天晴天的概率為 0.9,下雨的概率為 0.1。同樣在雨天開始。應該清楚的是,從給定的狀態,所有傳出的轉換應該總計 1.0,因為它是一個適當的分布。
表示此信息的另一種方法是通過轉移矩陣 P:

將其表示為矩陣的有趣之處在於,我們可以通過矩陣乘法來模擬馬爾可夫鏈。例如,假設我們從陽光明媚的狀態開始,我們可以將其表示為行向量:x(0)=[10]。這隱含地表示我們處於晴天狀態的概率為 1,因此處於下雨狀態的概率為 0。現在,如果我們執行矩陣乘法,我們可以在一步之後找出處於每個狀態的概率:

我們可以看到明天有 0.9 的機會晴天(根據我們的簡單模型),有 0.1 的機會下雨。實際上,我們可以繼續將轉換矩陣相乘,以在 k 步之後找到太陽/雨的機會:
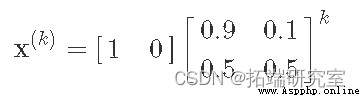
我們可以很容易地計算 x(k) 的各種 k 值,使用 numpy:
import numpy as np
Pa = nps.ardraasy([[0.9, 0.1], [0.5, 0.5]])
istsdatea = np.arasdray([1, 0])
siasdmulatase_markasdov(istaasdte, P, 10)



我們可以在這裡看到一個有趣的現象,當我們在狀態機中采取更多步驟時,晴天或下雨的概率似乎會收斂。您可能認為這與我們所處的初始狀態有關,但實際上並非如此。如果我們將初始狀態初始化為隨機值,我們將得到相同的結果:
siasmdulasteds_marksov(nap.arsdray([r, 1 - r]), P, 10)
x^(0) = [0.3653 0.6347]
x^(1) = [0.6461 0.3539]
x^(2) = [0.7584 0.2416]
x^(3) = [0.8034 0.1966]
x^(4) = [0.8214 0.1786]
x^(5) = [0.8285 0.1715]
x^(6) = [0.8314 0.1686]
x^(7) = [0.8326 0.1674]
x^(8) = [0.8330 0.1670]
x^(9) = [0.8332 0.1668]


這種穩態分布稱為 stationary distribution 通常用 π 表示。可以通過多種方式找到該穩態向量π。最直接的方法是在 nn 接近無窮大時取極限。

下一種方法就是求解方程。由於根據定義 q是穩態,因此乘以 P 應該返回相同的值:
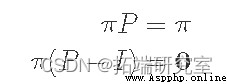
其中 I 是單位矩陣。如果您擴展我們的向量/矩陣符號,您會發現這只是一個方程組以及 π1,π2,...,πn 總和為 1 (即 π 形成概率分布)。在我們的例子中只有兩個狀態:π1+π2=1。
然而,並不是每個馬爾可夫鏈都有一個平穩的分布,甚至是唯一的 但是,如果我們向馬爾可夫鏈添加兩個額外的約束,我們可以保證這些屬性:
一個重要的定理說,如果馬爾可夫鏈是遍歷的,那麼它有一個唯一的穩態概率向量 ππ。在 MCMC 的上下文中,我們可以從任何狀態跳轉到任何其他狀態(以一定的有限概率),輕松滿足不可約性。
我們將使用的另一個有用的定義是 detailed balance and reversible Markov Chains. 如果存在滿足此條件的概率分布 π,則稱馬爾可夫鏈是可逆的(也稱為詳細平衡條件):
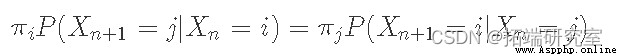
換句話說,從長遠來看,你從狀態 i 轉移到狀態 j 的次數比例,與你從狀態 j 轉移到狀態 i 的次數比例相同。事實上,如果馬爾可夫鏈是可逆的,那麼我們就知道它具有平穩分布(這就是我們使用相同符號 π 的原因)。
馬爾可夫鏈蒙特卡羅 (MCMC) 方法只是一類使用馬爾可夫鏈從特定概率分布(蒙特卡羅部分)中采樣的算法。他們通過創建一個馬爾可夫鏈來工作,其中限制分布(或平穩分布)只是我們想要采樣的分布。
這是一張可能有助於描述該過程的圖片. 想象一下,我們正在嘗試制作一個 MCMC 來嘗試使用 PDF f(x)對任意一維分布進行采樣。在這種情況下,我們的狀態將是沿 x 軸的點,而我們的轉換概率將是從一種狀態到另一種狀態的機會。這是情況的簡化圖:
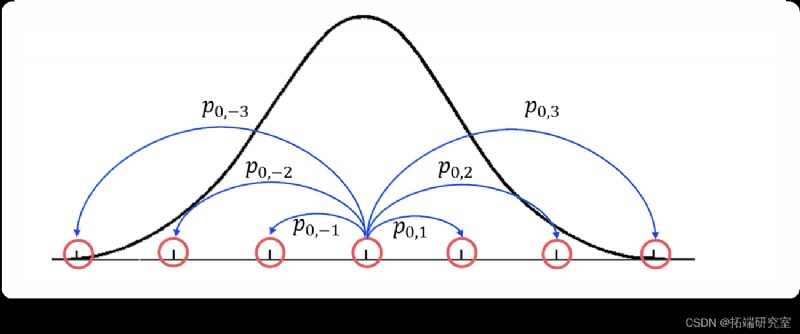
該圖顯示了我們試圖用粗黑線逼近的密度函數,以及使用從橙色狀態過渡的藍線的馬爾可夫鏈的一部分的可視化。特別是,對於 i=-3,-2,-1,1,2,3,只是從狀態 X0 到 Xi 的轉換。但是,x 軸線上的每個點實際上都是這個馬爾可夫鏈中的一個勢態。請注意,這意味著我們有一個無限的狀態空間,因此我們不能再將轉換很好地表示為矩陣。MCMC 方法的真正“訣竅”是我們想要設計狀態(或 x 軸上的點)之間的轉換概率,以便我們將大部分時間花在 f(x) 很大的區域中,並且在它較小的區域中的時間相對較少(即與我們的密度函數成精確比例)。
就我們的人物而言,我們希望將大部分時間花在中心周圍,而較少時間花在外面。事實上,如果我們模擬我們的馬爾可夫鏈足夠長的時間,狀態的限制分布應該近似於我們試圖采樣的 PDF。因此,使用 MCMC 方法進行采樣的基本算法為:
現在,我們在每個點 x 軸上花費的比例次數應該是我們試圖模擬的 PDF 的近似值,即如果我們繪制 x 值的直方圖,我們應該得到相同的形狀。
現在,在我們進入 MCMC 方法的具體算法之前,我想介紹另一種對概率分布進行采樣的方法,我們稍後將使用它,稱為 rejection sampling. 主要思想是,如果我們試圖從分布 f(x) 中采樣,我們將使用另一個工具分布 g(x) 來幫助從 f(x) 中采樣。唯一的限制是對於某些 M>1,f(x)<Mg(x)。它的主要用途是當 f(x) 的形式難以直接采樣時(但仍然可以在任何點 xx 對其進行評估)。
以下是算法的細分:
另一種看待它的方法是我們采樣點 x0 的概率。這與從 g 中采樣 x0 的概率乘以我們接受的次數的比例成正比,它簡單地由 f(x0) 和 Mg(x0) 之間的比率給出:

等式告訴我們對任意點進行采樣的概率與 f(x0) 成正比。在對許多點進行采樣並找到我們看到 x0 的次數比例之後,常數 M 被歸一化,我們得到了 PDF f(x) 的正確結果。
讓我們通過一個例子更直觀地看一下它。我們要從中采樣的目標分布 f(x) 是 double gamma 分布,基本上是一個雙邊伽馬分布。我們將使用正態分布 g(x) 作為我們的包絡分布。下面的代碼向我們展示了如何找到縮放常數 M,並為我們描繪了拒絕抽樣在概念上是如何工作的。
# 目標 = 雙伽馬分布
dsg = stats.dgamma(a=1)
# 生成PDF的樣本
x = np.linspace
# 繪圖
ax = df.plot(style=['--', '-'] 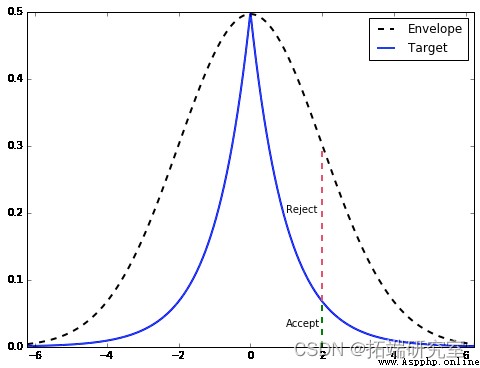
從圖中,一旦我們找到 g(x)的樣本(在這種情況下 x=2),我們從范圍等於 Mg(x) 高度的均勻分布中繪制. 如果它在目標 PDF 的高度內,我們接受它(綠色),否則拒絕(拒絕)。
下面的代碼為我們的目標雙伽馬分布實現拒絕采樣。它繪制標准化直方圖並將其與我們應該得到的理論 PDF 匹配。
# 從拒絕采樣算法生成樣本
sdampales = [rejeasdctioan_samplaing for x in range(10000)]
# 繪制直方圖與目標 PDF
df['Target'].plot
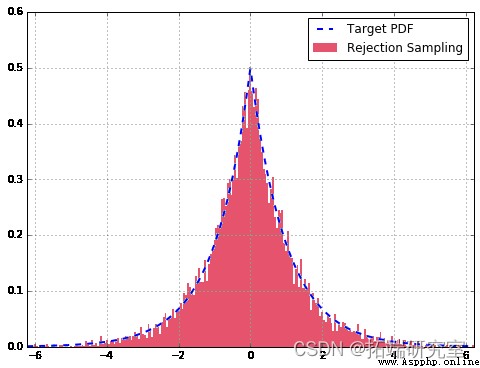
總的來說,我們的拒絕采樣器非常適合。與理論分布相比,抽取更多樣本會改善擬合。
拒絕抽樣的很大一部分是它很容易實現(在 Python 中只需幾行代碼),但有一個主要缺點:它很慢。
這 Metropolis-Hastings Algorithm (MH) 是一種 MCMC 技術,它從難以直接采樣的概率分布中抽取樣本。與拒絕抽樣相比,對 MH 的限制實際上更加寬松:對於給定的概率密度函數 p(x),我們只要求我們有一個 與 p成正比的函數 f(x)f(x) (x)p(x)!這在對後驗分布進行采樣時非常有用。
為了推導出 Metropolis-Hastings 算法,我們首先從最終目標開始:創建一個馬爾可夫鏈,其中穩態分布等於我們的目標分布 p(x)。就馬爾可夫鏈而言,我們已經知道狀態空間將是什麼:概率分布的支持,即 x 值。因此(假設馬爾可夫鏈的構造正確)我們最終得到的穩態分布將只是 p(x)。剩下的是確定這些 x 值之間的轉換概率,以便我們可以實現這種穩態行為。
馬爾可夫鏈的詳細平衡條件,這裡用另一種方式寫成:
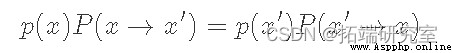
這裡 p(x)是我們的目標分布,P(x→x′) 是從點 x到點 x′ 的轉移概率。所以我們的目標是確定P(x→x′)的形式。既然我們要構建馬爾可夫鏈,讓我們從使用等式 5 作為該構建的基礎開始。請記住,詳細的平衡條件保證我們的馬爾可夫鏈將具有平穩分布(它存在)。此外,如果我們也包括遍歷性(不以固定間隔重復狀態,並且每個狀態最終都能夠達到任何其他狀態),我們將建立一個具有唯一平穩分布 p(x)的馬爾可夫鏈.
我們可以將方程重新排列為:
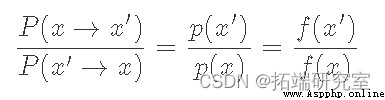
這裡我們使用 f(x)來表示一個 與 p(x)成正比的函數。這是為了強調我們並不明確需要 p(x),只是需要與它成比例的東西,這樣比率才能達到相同的效果。現在這裡的“技巧”是我們將把 P(x→x′)分解為兩個獨立的步驟:一個提議分布 g(x→x′) 和接受分布 A(x→x′)(類似於拒絕抽樣的工作原理)。由於它們是獨立的,我們的轉移概率只是兩者的乘積:
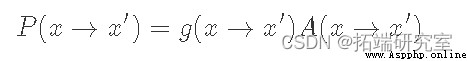
此時,我們必須弄清楚 g(x)和 A(x) 的合適選擇是什麼。由於 g(x) 是“建議分布”,它決定了我們可能采樣的下一個點。因此,重要的是它具有與我們的目標分布 p(x)(遍歷性條件)相同的支持。這裡的一個典型選擇是以當前狀態為中心的正態分布。現在給定一個固定的提議分布 g(x),我們希望找到一個匹配的 A(x)。
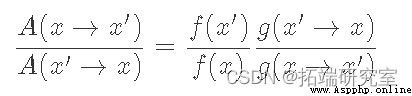
雖然不明顯,但滿足公式 的 A(x) 的典型選擇是:
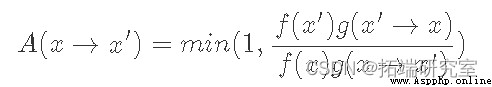
我們可以通過考慮 f(x′)g(x′→x)小於等於 1 和大於 1 的情況。當小於等於 1 時,它的倒數大於 1,因此 LHS 的分母,A(x′→ x), 等式 8 為 1,而分子等於 RHS。或者,當f(x′)g(x′→x)是大於 1 LHS 的分子是 1,而分母正好是 RHS 的倒數,導致 LHS 等於 RHS。
這樣,我們已經證明,我們創建的馬爾可夫鏈的穩定狀態將等於我們的目標分布 (p(x)),因為詳細的平衡條件通過構造得到滿足。所以整體算法將是(與上面的 MCMC 算法非常匹配):
在我們繼續實現之前,我們需要討論關於 MCMC 方法的兩個非常重要的話題。第一個主題與我們選擇的初始狀態有關。由於我們隨機選擇 xx 的值,它很可能位於 p(x) 非常小的區域(想想我們的雙伽馬分布的尾部)。如果從這裡開始,它可能會花費不成比例的時間來遍歷低密度的 x 值,從而錯誤地給我們一種感覺,即這些 x 值應該比它們更頻繁地出現。所以解決這個問題的方法是“預燒”采樣器通過生成一堆樣本並將它們扔掉。樣本的數量將取決於我們試圖模擬的分布的細節。
我們上面提到的第二個問題是兩個相鄰樣本之間的相關性。由於根據我們的轉換函數 P(x→x′)的定義,繪制 x′ 取決於當前狀態 x。因此,我們失去了樣本的一項重要屬性:獨立性。為了糾正這一點,我們抽取 Tth 個樣本,並且只記錄最後抽取的樣本。假設 T 足夠大,樣本應該是相對獨立的。與預燒一樣,T 的值取決於目標和提議分布。
讓我們使用上面的雙伽馬分布示例。讓我們將我們的提議分布定義為以 x 為中心、標准差為 2、N(x, 2) 的正態分布(記住 x 是當前狀態):
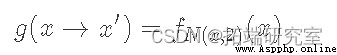
給定 f(x) 與我們的基礎分布 p(x) 成比例,我們的接受分布如下所示:
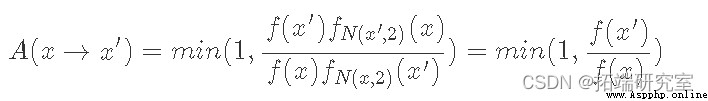
由於正態分布是對稱的,因此正態分布的 PDF 在其各自點進行評估時會相互抵消。現在讓我們看一些代碼:
# 模擬與雙伽馬分布成比例的 f(x)
f = ambd x: g.df(x* mat.i
采樣器 = mhspler()
# 樣本
sames = [nex(saper) for x in range(10000)]
# 繪制直方圖與目標 PDF
df['Target'].plot 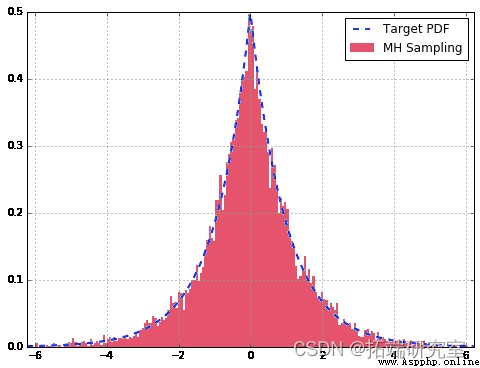
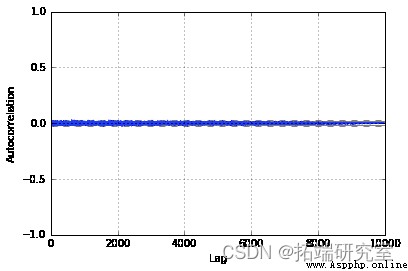
來自我們的 MH 采樣器的樣本很好地近似於我們的雙伽馬分布。此外,查看自相關圖,我們可以看到它在整個樣本中非常小,表明它們是相對獨立的。如果我們沒有為 T 選擇一個好的值或沒有預燒期,我們可能會在圖中看到較大的值。
我希望你喜歡這篇關於使用拒絕抽樣和使用 Metropolis-Hastings 算法進行 MCMC 抽樣的簡短文章。

最受歡迎的見解
1.使用R語言進行METROPLIS-IN-GIBBS采樣和MCMC運行
2.R語言中的Stan概率編程MCMC采樣的貝葉斯模型
3.R語言實現MCMC中的Metropolis–Hastings算法與吉布斯采樣
4.R語言BUGS JAGS貝葉斯分析 馬爾科夫鏈蒙特卡洛方法(MCMC)采樣
5.R語言中的block Gibbs吉布斯采樣貝葉斯多元線性回歸
6.R語言Gibbs抽樣的貝葉斯簡單線性回歸仿真分析
7.R語言用Rcpp加速Metropolis-Hastings抽樣估計貝葉斯邏輯回歸模型的參數
8.R語言使用Metropolis- Hasting抽樣算法進行邏輯回歸
9.R語言中基於混合數據抽樣(MIDAS)回歸的HAR-RV模型預測GDP增長